
如图,正方形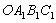 的边长为2,以
的边长为2,以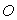 为圆心、
为圆心、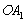 为半径作弧
为半径作弧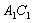 交
交 于点
于点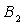 ,设弧
,设弧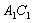 与边
与边 、
、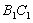 围成的阴影部分面积为
围成的阴影部分面积为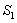 ;然后以
;然后以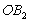 为对角线作正方形
为对角线作正方形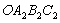 ,又以
,又以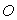 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交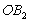 于点
于点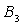 ,设弧
,设弧 与边
与边 、
、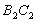 围成的阴影部分面积为
围成的阴影部分面积为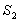 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边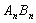 、
、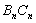 围成的阴影部分面积为
围成的阴影部分面积为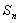 .则:(1)
.则:(1)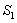 = ;(2)
= ;(2)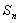 = .
= .

科目:初中数学 来源: 题型:
如图,现有边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC 于H,折痕为EF,联结BP、BH.
于H,折痕为EF,联结BP、BH.
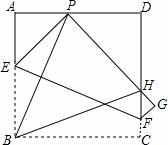
(1)求证:∠APB=∠BPH;
(2)求证:AP+ HC=PH;
HC=PH;
(3)当AP=1时,求PH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3,则下列结论不一定成立的是( )

A.S1>S2+S3 B.△AOM∽△DMN C.∠MBN=45° D.MN=AM+CN
查看答案和解析>>
科目:初中数学 来源: 题型:
已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF
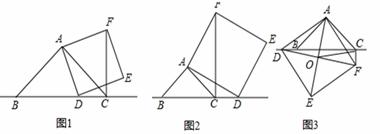
(1)如图1,当点D在线段BC上时.求证CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2 ,对角线AE,DF相交于点O,连接OC 求OC的长度.
,对角线AE,DF相交于点O,连接OC 求OC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:对于实数a,符号[a]表示不大于a的最大整数.
 例如:[5.7]=5,[5]=5,[-π]=-4.
例如:[5.7]=5,[5]=5,[-π]=-4.
(1)如果[a]=-2,那么a的取值范围是 ___________.
(2)如果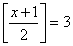
 ,满足条件的所有正整数
,满足条件的所有正整数 x有___________
x有___________ _.
_.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线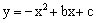 的顶点为D(﹣1,4),与
的顶点为D(﹣1,4),与 轴交于点C(0,3),与
轴交于点C(0,3),与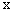 轴交于A,B两点(点A在点B的左侧)。
轴交于A,B两点(点A在点B的左侧)。
(1)求抛物线的解析式;
(2)连接AC,CD,AD,试证明△ACD为直角三角形;
(3)若点E在抛物线上,EF⊥x轴于点F,以A、E、F为顶点的三角形与△ACD相似,试求出所有满足条件的点E的坐标。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com