
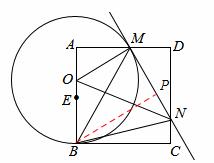
如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3,则下列结论不一定成立的是( )

A.S1>S2+S3 B.△AOM∽△DMN C.∠MBN=45° D.MN=AM+CN
A.
【解析】(1)如答图1,过点M作MP∥AO交ON于点P,∵点O是线段AE上的一个动点,
当AM=MD时,S梯形ONDA=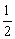 (OA+DN)•ADS△MNO=
(OA+DN)•ADS△MNO=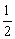 MP•AD,∵
MP•AD,∵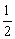 (OA+DN)=MP,∴S△MNO=
(OA+DN)=MP,∴S△MNO=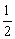 S梯形ONDA,∴S1=S2+S3,∴不一定有S1>S2+S3. 故A不一定成立.
S梯形ONDA,∴S1=S2+S3,∴不一定有S1>S2+S3. 故A不一定成立.
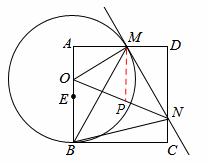
(2)∵MN是⊙O的切线,∴OM⊥MN,又∵四边形ABC D为正方形,
D为正方形,
∴∠A=∠D=90°,∠AMO+∠DMN=90°,∠AMO+∠AOM=90°.∴∠AOM=∠DMN.
在△AMO和△DMN中,∵ ,∴△AMO∽△DMN.故B成立.
,∴△AMO∽△DMN.故B成立.
(3)如答图2,过点B作BP⊥MN于点P,∵MN,BC是⊙O的切线,
∴∠PMB=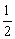 ∠MOB,∠CBM=
∠MOB,∠CBM=
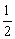 ∠MOB.∵AD∥BC,∴∠CBM=∠AMB. ∴∠AMB=∠PMB.
∠MOB.∵AD∥BC,∴∠CBM=∠AMB. ∴∠AMB=∠PMB.
在Rt△MAB和Rt△MPB中,∵ ,
,
∴Rt△MAB≌Rt△MPB(AAS).∴AM=MP,∠ABM=∠MBP,BP=AB=BC.
在Rt△BPN和Rt△BCN中,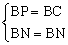 ,∴Rt△BPN≌Rt△BCN(HL).
,∴Rt△BPN≌Rt△BCN(HL).
∴PN=CN,∠PBN=∠CBN. ∴∠MBN=∠MBP+∠PBN.∴MN=MN+PN=AM+CN.故C,D成立.
综上所述,A不一定成立.
故选A.


科目:初中数学 来源: 题型:
一款手机连续两次降价,由原来的1299元降到688元,设平均每次降价的百分率为x,则列方程为( )
A.688(1+x)2=1299 B.1299(1+x)2=688
C.688(1-x)2=1299 D.1299(1-x)2=688
查看答案和解析>>
科目:初中数学 来源: 题型:
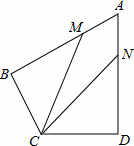
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2, 则tan∠MCN=
则tan∠MCN=
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形ABCD和正方形AEFG有公共的顶点A,连BG、DE,M为DE的中点,连AM.
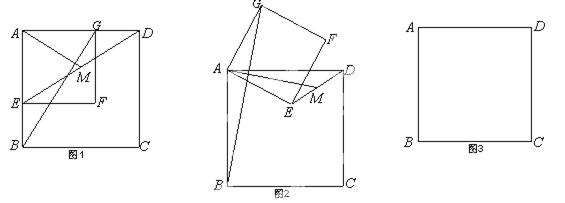
(1)如图1,AE、AG分别与AB、AD重合时,AM和BG的大小和位置关系分别是 、_ ____;
(2)将图1中的正方形AEFG绕A点旋转到如图2,则(1)中的结论是否仍成立?试证明你的结论;
(3)若将图1中的正方形AEFG绕A点逆时针旋转到正方形ABCD外时,则AM和BG的大小和位置关系分别是__________、____________,请你在图3中画出图形,并直 接写出结论,不要求证明.
接写出结论,不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
正方形ABCD中,点P从点C出发沿着正方形的边依次经过点D,A向终点B运动,运动的路程为x(cm),△PBC的面积为y(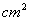 ),y随x变化的图象可能是( )
),y随x变化的图象可能是( )
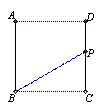

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形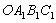 的边长为2,以
的边长为2,以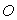 为圆心、
为圆心、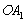 为半径作弧
为半径作弧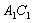 交
交 于点
于点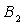 ,设弧
,设弧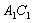 与边
与边 、
、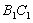 围成的阴影部分面积为
围成的阴影部分面积为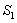 ;然后以
;然后以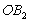 为对角线作正方形
为对角线作正方形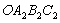 ,又以
,又以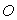 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交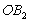 于点
于点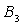 ,设弧
,设弧 与边
与边 、
、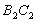 围成的阴影部分面积为
围成的阴影部分面积为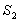 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边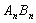 、
、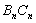 围成的阴影部分面积为
围成的阴影部分面积为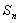 .则:(1)
.则:(1)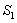 = ;(2)
= ;(2)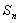 = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
一个四位数, 其各位上的四个数字的平方和等于个位、千位数字乘积的2倍与十位、百位数字乘积的2倍之和,且个位与十位数字相同
其各位上的四个数字的平方和等于个位、千位数字乘积的2倍与十位、百位数字乘积的2倍之和,且个位与十位数字相同 ,符合上述条件的四位数共有 个。
,符合上述条件的四位数共有 个。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com