
如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C.

(1)求经过A、B、C三点的抛物线所对应的函数解析式;
(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;
(3)试说明直线MC与⊙P的位置关系,并证明你的结论.
(1)y=-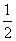 x2+
x2+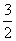 x+2,(2)
x+2,(2)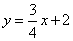 .(3)MC与⊙P的位置关系是相切.证明见解析.
.(3)MC与⊙P的位置关系是相切.证明见解析.
【解析】 (1)连接PC,
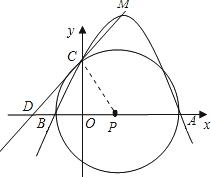
∵A(4,0),B(-1,0),∴AB=5,半径PC=PB=PA=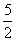 ,∴OP=
,∴OP=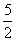 -1=
-1=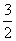 ,
,
在△CPO中,由勾股定理得:OC=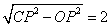 ,∴C(0,2),
,∴C(0,2),
设经过A、B、C三点抛物线解析式是y=a(x-4)(x+1),
把C(0,2)代入得:2=a(0-4)(0+1),∴a=-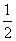 ,
,
∴y=-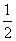 (x-4)(x+1)=-
(x-4)(x+1)=-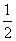 x2+
x2+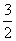 x+2,
x+2,
(2)y=-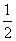 x2+
x2+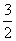 x+2=-
x+2=-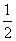 (x-
(x-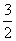 )2+
)2+ ,M(
,M(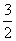 ,
, ),
),
设直线MC对应函数表达式是y=kx+b,把C(0,2),M(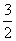 ,
, )代入得:
)代入得:
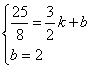 ,解得:
,解得: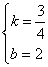 ,∴
,∴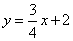 .
.
(3)MC与⊙P的位置关系是相切.
设直线MC交x轴于D,当y=0时,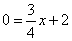 ,∴x=-
,∴x=-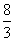 ,OD=
,OD=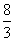 ,
,
∴D(-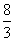 ,0),在△COD中,由勾股定理得:CD2=22+(
,0),在△COD中,由勾股定理得:CD2=22+(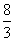 )2=
)2=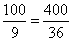 ,
,
PC2=(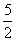 )2=
)2=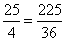 ,PD2=(
,PD2=(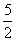 +
+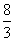 -1)2=
-1)2=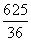 ,∴CD2+PC2=PD2,∴∠PCD=90°,
,∴CD2+PC2=PD2,∴∠PCD=90°,
∴PC⊥DC,∵PC为半径,∴MC与⊙P的位置关系是相切.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
如图,在⊿ABC中,∠A﹤90°,∠C=30°,AB=4,BC=6,E为AB的中点,P为AC边上一动点,将⊿ABC绕点B逆时针旋转 角(
角(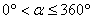 )得到
)得到 ,点P的对应点为
,点P的对应点为
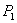 ,连
,连 ,在旋转过程中,线段
,在旋转过程中,线段 的长度的最小值是 .
的长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,设∠BAC=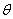 (0°<
(0°<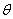 <90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A
<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A 开始,用等长的小棒依次向右摆放,其中 A
开始,用等长的小棒依次向右摆放,其中 A A
A 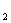 为第一根小棒,且 A
为第一根小棒,且 A A
A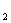 =AA
=AA

(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)若已经摆放了3根小棒,则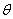 1 = ,
1 = ,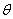 2= ,
2= , 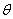 3= ;(用含
3= ;(用含 的式子表示)
的式子表示)
(3)若只能摆放4根小棒,求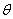 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
正方形ABCD中,点P从点C出发沿着正方形的边依次经过点D,A向终点B运动,运动的路程为x(cm),△PBC的面积为y(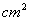 ),y随x变化的图象可能是( )
),y随x变化的图象可能是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
在矩形ABCD中,AB=1,AD=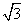 ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE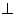 BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
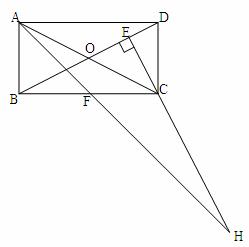
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,二次函数y=-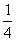 x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
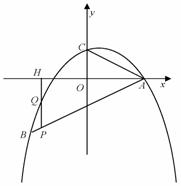
(1)求此二次函数的解析式;
(2)证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图像及x轴于Q、H两点,试问:是否存在这样的点 P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com