
【题目】如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q,∠BPQ的度数是_____;若PQ=3,EP=1,则DA的长是_____.
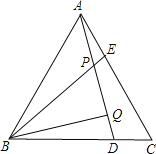
【答案】60°, 7.
【解析】
根据等边三角形的性质,通过全等三角形的判定定理SAS证出△AEB≌△CDA,利用全等三角形的对应角相等和三角形外角的性质求得∠BPQ=60°,然后可得∠PBQ=30°,由“30度角所对的直角边是斜边的一半”得到2PQ=BP=6,则易求BE=BP+PE=7.
解:∵△ABC为等边三角形,
∴AB=CA,∠BAE=∠C=60°,
∴在△AEB与△CDA中,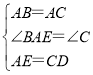 ,
,
∴△AEB≌△CDA(SAS);
∴∠ABE=∠CAD,AD=BE,
∴∠BAD+∠ABP=∠BAD+∠CAD=∠BAC=60°,
∴∠BPQ=∠BAD+∠ABP=60°,
∵BQ⊥AD,
∴∠PBQ=30°,
∴PQ=![]() BP=3,
BP=3,
∴BP=6,
∵EP=1,
∴BE=BP+PE=7,
∴DA=BE=7.
故答案为:60°,7.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②DE长度的最小值为4;③四边形CDFE的面积保持不变;④△CDE面积的最大值为8.其中正确的结论是( )
A.①②③B.①③C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,若MN=2,则NF=___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=40°,点D在BC边上(不与C、D点重合),点P、点Q分别是AC、AB边上的动点,当△DPQ的周长最小时,则∠PDQ的度数为( )

A. 140°B. 120°C. 100°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.

![]() 求这条直线的函数关系式及点
求这条直线的函数关系式及点![]() 的坐标.
的坐标.
![]() 在
在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
![]() 过线段
过线段![]() 上一点
上一点![]() ,作
,作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限,点
在第一象限,点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级三班学生苏琪为帮助同桌万宇巩固“平面直角坐标系四个象限内及坐标轴上的点的坐标特点”这一基础知识,在三张完全相同且不透明的卡片正面分别写上了﹣3,0,2三个数字,背面向上洗匀后随机抽取一张,将卡片上的数字记为a,再从剩下的两张中随机取出一张,将卡片上的数字记为b,然后叫万宇在平面直角坐标系中找出点M(a,b)的位置.
(1)请你用树状图帮万宇同学进行分析,并写出点M所有可能的坐标;
(2)求点M在第二象限的概率;
(3)张老师在万宇同学所画的平面直角坐标系中,画了一个半径为3的⊙O,过点M能作多少条⊙O的切线?请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形 ![]() 中,
中,![]() ,
,![]() ,
,![]() 是矩形
是矩形 ![]() 中能剪出的最大圆,矩形
中能剪出的最大圆,矩形 ![]() 固定不动,
固定不动,![]() 从如图位置开始沿射线
从如图位置开始沿射线 ![]() 方向平移,当
方向平移,当 ![]() 与矩形
与矩形 ![]() 重叠部分面积为
重叠部分面积为 ![]() 面积一半时,平移距离为________________.
面积一半时,平移距离为________________.
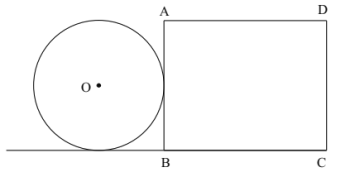
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=![]() x+6.
x+6.
(1)求直线y=![]() x+6与x轴、y轴交点坐标;
x+6与x轴、y轴交点坐标;
(2)求出一次函数图象与坐标轴所围成的三角形的面积;
(3)求坐标原点O到直线y=![]() x+6的距离.
x+6的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,BD和AC交于点O,下列结论错误的是( )

A.AC垂直平分BDB.图中共有三对全等三角形
C.∠OCD=∠ODCD.四边形ABCD的面积等于![]() ACBD
ACBD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com