
【题目】如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,若MN=2,则NF=___________

【答案】1
【解析】
连接AN、AM,根据等腰三角形性质可知∠B=∠C=30°,利用线段垂直平分线定理可得BM=AM,AN=CN,根据等边对等角可知∠B=∠MAB,∠NAC=∠C,即可知道△AMN是等边三角形,进而得到AN的长,利用直角三角形中30°角所对的直角边是斜边的一半,即可求得NF的长.
如图,连接AN、AM,

∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵ME、NF分别垂直平分线段AB、AC
∴BM=AM,AN=CN,
∴∠B=∠MAB=30°,∠NAC=∠C=30°,
∴∠AMN=∠MAN=∠MNA=60°
∴△AMN是等边三角形,
∴AN=MN=2
在Rt△ANF中,∠NAF=30°
∴NF=![]() AN=1
AN=1
故答案为:1


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】某校在八年级(1)班学生中开展对于“我国国家公祭日”知晓情况的问卷调调查. 问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.
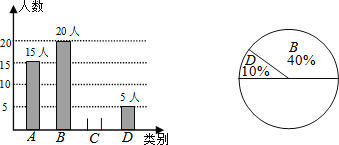
请根据上述信息解答下列问题:
(1)该班参与问卷调查的人数有 人;
(2)补全条形统计图;
(3)求C类人数占总调查人数的百分比;
(4)求扇形统计图中A类所对应扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() ,且3x+4z﹣2y=40,求x,y,z的值;
,且3x+4z﹣2y=40,求x,y,z的值;
(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量某教学楼CD的高度,小明在教学楼前距楼基点C,12米的点A处测得楼顶D的仰角为50°,小明又沿CA方向向后退了3米到点B处,此时测得楼顶D的仰角为40°(B、A、C在同一水平线上),依据这些数据小明能否求出教学楼的高度?若能求,请你帮小明求出楼高;若不能求,请说明理由.(![]() 取2.24)
取2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且∠EAF=60°,请探究图中线段BE,EF,FD之间的数量关系是什么?

小明探究此问题的方法是:延长FD到点G,使DG=BE,连结AG.先证明△ABE≌△ADG,得AE=AG;再由条件可得∠EAF=∠GAF,证明△AEF≌△AGF,进而可得线段BE,EF,FD之间的数量关系是 .
(2)拓展应用:
如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,请给出证明;若不成立,请说明理由.
∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC.
(1)若AB=4,AC=5,则BC边的取值范围是 ;
(2)点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.
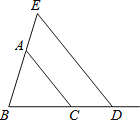
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,球路的最高点B(8,9),则这个二次函数的表达式为______,小孩将球抛出了约______米(精确到0.1m).
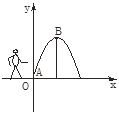
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q,∠BPQ的度数是_____;若PQ=3,EP=1,则DA的长是_____.
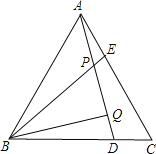
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD.

(1)求证:∠BDC=![]() ∠BAC;
∠BAC;
(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com