
【题目】如图,在ABCD中,DC>AD,四个角的平分线AE,DE,BF,CF的交点分别是E,F,过点E,F分别作DC与AB间的垂线MM'与NN',在DC与AB上的垂足分别是M,N与M′,N′,连接EF.
(1)求证:四边形EFNM是矩形;
(2)已知:AE=4,DE=3,DC=9,求EF的长.
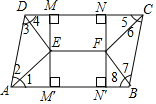
【答案】(1)证明见解析;(2)EF=4
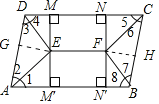
【解析】(1)要说明四边形EFNM是矩形,有ME⊥CD,FN⊥CD条件,还缺ME=FN,过点E、F分别作AD、BC的垂线,垂足分别是G、H.利用角平分线上的点到角两边的距离相等可得结论;
(2)利用平行四边形的性质,证明直角△DEA,并求出AD的长.利用全等证明△GEA≌△CNF,△DME≌△DGE从而得到DM=DG,AG=CN,再利用线段的和差关系,求出MN的长得结论.
(1)如图,过点E、F分别作AD、BC的垂线,垂足分别是G、H,
∵∠3=∠4,∠1=∠2,EG⊥AD,EM⊥CD,EM′⊥AB,
∴EG=ME,EG=EM′,
∴EG=ME=ME′=![]() MM′,
MM′,
同理可证:FH=NF=N′F=![]() NN′,
NN′,
∵CD∥AB,MM′⊥CD,NN′⊥CD,
∴MM′=NN′,
∴ME=NF=EG=FH,
又∵MM′∥NN′,MM′⊥CD,
∴四边形EFNM是矩形;
(2)∵DC∥AB,
∴∠CDA+∠DAB=180°,
∵∠3=![]() ∠CDA ,∠2=
∠CDA ,∠2=![]() ∠DAB,
∠DAB,
∴∠3+∠2=90°,
在Rt△DEA,∵AE=4,DE=3,
∴AB=![]() =5,
=5,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB,
又∵∠2=![]() ∠DAB,∠5=
∠DAB,∠5=![]() ∠DCB,
∠DCB,
∴∠2=∠5,
由(1)知GE=NF,
在Rt△GEA和Rt△CNF中
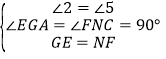 ,
,
∴△GEA≌△CNF,
∴AG=CN,
在Rt△DME和Rt△DGE中,
∵DE=DE,ME=EG,
∴△DME≌△DGE,
∴DG=DM,
∴DM+CN=DG+AG=AB=5,
∴MN=CD﹣DM﹣CN=9﹣5=4,
∵四边形EFNM是矩形,
∴EF=MN=4.


科目:初中数学 来源: 题型:
【题目】某地电话拨号上网有两种收费方式,用户可以任意选择其中一种:第一种是计时制,0.05元/分; 第二种是包月制,69元/月(限一部个人住宅电话上网).此外,每一种上网方式都得加收通讯费0.02元/分.
(1)若小明家今年三月份上网的时间为![]() 小时,请你分别写出两种收费方式下小明家应该支付的费用;
小时,请你分别写出两种收费方式下小明家应该支付的费用;
(2)若小明估计自家一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
|
|
|
|
|
| … |
(1)可求得![]() ,第
,第![]() 个格子中的数为 ;
个格子中的数为 ;
(2)若前![]() 个格子中所填整数之和
个格子中所填整数之和![]() ,则
,则![]() 的值为多少?若
的值为多少?若![]() 的值为多少?
的值为多少?
(3)若![]() ,则
,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是( )

A. 6<t≤8 B. 6≤t≤8 C. 10<t≤12 D. 10≤t≤12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读图,回答问题
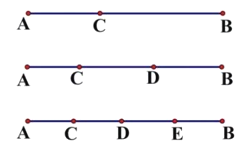
(1)在线段![]() 上取一点
上取一点![]() ,共有 条线段;
,共有 条线段;
(2)在线段![]() 上取两点
上取两点![]() ,共有 条线段;
,共有 条线段;
(3)在线段![]() 上取三点
上取三点![]() ,共有 条线段;
,共有 条线段;
(4)在线段![]() 上取
上取![]() 个点,共有 条线段.
个点,共有 条线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是网上盛传的一个关于数学的诡辩问题截图,表1是它的示意表.我们一起来解答“为什么多出了![]() 元”.
元”.

表1
花去 | 剩余 | |
买牛肉 |
|
|
买猪脚 |
|
|
买蔬菜 |
|
|
买调料 |
|
|
总计 |
|
|
(1)为了解释“剩余金额总计”与“我手里有![]() 元”无关,按要求填写表2中的空格.
元”无关,按要求填写表2中的空格.
表2
花去 | 剩余 | |
买牛肉 |
|
|
买猪脚 |
|
|
买蔬菜 | 元 | 元 |
买调料 | 元 |
|
总计 |
|
|
表3
花去 | 剩余 | |
买物品1 |
|
|
买物品2 |
|
|
买物品3 |
|
|
买物品4 |
|
|
总计 |
|
|
(2)如表3中,直接写出以下各代数式的值:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(3)如表3中,![]() 都是正整数,则
都是正整数,则![]() 的最大值等于 ;最小值等于 .由此可以知道“为什么多出了
的最大值等于 ;最小值等于 .由此可以知道“为什么多出了![]() 元”只是一个诡辩而已.
元”只是一个诡辩而已.
(4)我们将“花去”记为“![]() ”,“剩余”记为“
”,“剩余”记为“![]() ”,请在表4中将表1数据重新成号.
”,请在表4中将表1数据重新成号.
花去 | 剩余 | |
买牛肉 | 元 | 元 |
买猪脚 | 元 | 元 |
买蔬菜 | 元 | 元 |
买调料 | 元 | 元 |
总计 | 元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.
(1)求购买1个排球、1个篮球的费用分别是多少元?
(2)若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
发现:∠POQ=________时,PQ有最大值,最大值为________;
思考:(1)如图2,若P是OB中点,且QP⊥OB于点P,求![]() 的长;
的长;
(2)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在OA的延长线上,求阴影部分面积;
探究:如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com