
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A的坐标为(0,2),点p的坐标为(m,0)且m>0,一开口向上的抛物线以P为顶点,且经过点A.
如图,在平面直角坐标系中,点A的坐标为(0,2),点p的坐标为(m,0)且m>0,一开口向上的抛物线以P为顶点,且经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 序号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
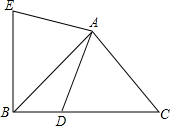 在等腰Rt△ABC中,∠A=90°,AC=AB=2,D是BC边上的点且BD=$\frac{1}{3}$CD,连接AD,把AD绕着点A顺时针旋转90°得到线段AE,连接BE,则点B到AD的距离为$\frac{\sqrt{10}}{5}$.
在等腰Rt△ABC中,∠A=90°,AC=AB=2,D是BC边上的点且BD=$\frac{1}{3}$CD,连接AD,把AD绕着点A顺时针旋转90°得到线段AE,连接BE,则点B到AD的距离为$\frac{\sqrt{10}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
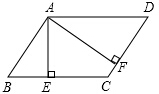 如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是80.
如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是80.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平角是一条线段 | B. | 周角是一条射线 | ||
| C. | 两个锐角的和不一定小于平角 | D. | 反向延长射线OA,就形成一个平角 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
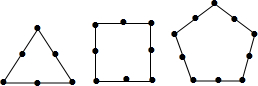 墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子.
墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com