练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    三角形的两边长是3和4，第三边长是方程x2﹣12x+35=0的根，则三角形的周长为(     )

    A．12     B．13     C．14     D．12或14


    A【考点】解一元二次方程-因式分解法；三角形三边关系．

    【专题】计算题．

    【分析】首先求出方程的根，再根据三角形三边关系定理，确定第三边的长，进而求其周长和面积．

    【解答】解：解方程x2﹣12x+35=0，得x1=5，x2=7，即第三边的边长为5或7．

    ∵1＜第三边的边长＜7，

    ∴第三边的边长为5．

    ∴这个三角形的周长是3+4+5=12．

    故选A．

    【点评】本题考查了三角形的三边关系．已知三角形的两边，则第三边的范围是：大于已知的两边的差，而小于两边的和．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    在解方程时，去分母正确的是（  ）

    A.         B.

    C.         D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    数学老师布置了一道思考题“计算：（﹣）”，小明仔细思考了一番，用了一种不同的方法解决了这个问题．

    小明的解法：原式的倒数为（）=（）×（﹣12）=﹣4+10=6，

    所以（﹣）=．

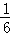    （1）请你判断小明的解答是否正确，并说明理由．

    （2）请你运用小明的解法解答下面的问题．

    计算：（﹣）．

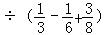    查看答案和解析>>

    科目：初中数学 来源： 题型：


    x2﹣x﹣2=0；（公式法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


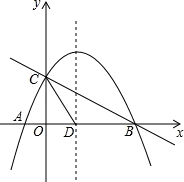
    如图，直线y1=﹣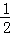x+2与x轴，y轴分别交于B，C，抛物线y=ax2+bx+c（a≠0）经过点A，B，C，点A坐标为（﹣1，0）．

    （1）求抛物线的解析式；

    （2）抛物线的对称轴与x轴交于点D，连接CD，点P是直线BC上方抛物线上的一动点（不与B，C重合），当点P运动到何处时，四边形PCDB的面积最大？求出此时四边形PCDB面积的最大值和点P坐标；

    （3）在抛物线上的对称轴上是否存在一点Q，使△QCD是以CD为腰的等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc＞0；②﹣b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0；其中正确的结论有(     )

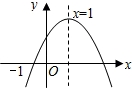
    A．1个  B．2个   C．3个  D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y=2x2+3x﹣9的图象与x轴交点的横坐标是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，若AD⊥BC，点E是BC边上一点，且不与点B、C、D重合，则AD是几个三角形的高线(     )

    A．4个  B．5个   C．6个  D．8个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：（3x+2）（3x﹣2）﹣（3﹣5x）（x﹣1）﹣（2x﹣1）2，其中x=﹣2．

    查看答案和解析>>

    同步练习册答案