
【题目】如图在直角坐标系中,四边形ABCO为正方形,A点的坐标为(a,0),D点的坐标为(0,b),且a,b满足(a﹣3)2+|b﹣![]() |=0.
|=0.
(1)求A点和D点的坐标;
(2)若∠DAE=![]() ∠OAB,请猜想DE,OD和EB的数量关系,说明理由.
∠OAB,请猜想DE,OD和EB的数量关系,说明理由.
(3)若∠OAD=30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明.

【答案】(1)D(0,![]() ),A(3,0);(2)DE=OD+EB; 理由见解析;(3)点P的坐标为:∴P(﹣3,0)或(0,3
),A(3,0);(2)DE=OD+EB; 理由见解析;(3)点P的坐标为:∴P(﹣3,0)或(0,3![]() )或(0,﹣
)或(0,﹣![]() )或(1,0)或(3+2
)或(1,0)或(3+2![]() ,0)或(3﹣2
,0)或(3﹣2![]() ,0).证明见解析.
,0).证明见解析.
【解析】
(1)根据完全平方式和绝对值的非负性确定a,b的值,从而求点的坐标;
(2)在CO的延长线上找一点F,使OF=BE,连接AF,通过△AOF≌△ABE,得到AF=AE,∠OAF=∠BAE,等量代换得到∠DAF=∠EAD,进而证明△AFD≌△AED,从而求解;
(3)分三种情形讨论求解:AD=DP或AD=AP或PD=AP,分别画图根据AD和OA的长确定点P的坐标.
(1)∵(a﹣3)2+|b﹣![]() |=0,
|=0,
∴a=3,b=![]() ,
,
∴D(0,![]() ),A(3,0);
),A(3,0);
(2)DE=OD+EB; 理由如下:
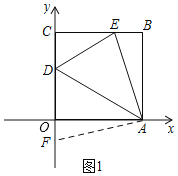
如图1,在CO的延长线上找一点F,使OF=BE,连接AF,
在△AOF和△ABE中,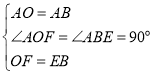 ,
,
∴△AOF≌△ABE(SAS),
∴AF=AE,∠OAF=∠BAE,
又∵∠OAB=90°,∠DAE=![]() ,
,
∴∠BAE+∠DAO=45°,
∴∠DAF=∠OAF+∠DAO=45°,
∴∠DAF=∠EAD,
在△AFD和△AED中,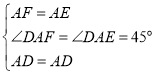 ,
,
∴△AFD≌△AED(SAS),
∴DF=DE=OD+EB;
(3)有3种情况共6个点:
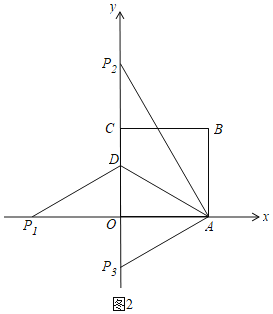
①当DA=DP时,如图2,
Rt△ADO中,OD=![]() ,OA=3,
,OA=3,
∴AD=![]() ,
,
∴P1(﹣3,0),P2(0,3![]() ),P3(0,﹣
),P3(0,﹣![]() );
);
②当AP4=DP4时,如图3,
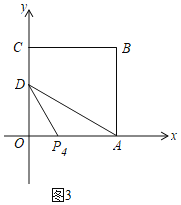
∴∠ADP4=∠DAP4=30°,
∴∠OP4D=60°,
Rt△ODP4中,∠ODP4=30°,OD=![]() ,
,
∴OP4=1,
∴P4(1,0);
③当AD=AP时,如图4,
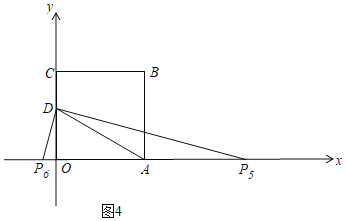
∴AD=AP5=AP6=2![]() ,
,
∴P5(3+2![]() ,0),P6(3﹣2
,0),P6(3﹣2![]() ,0),
,0),
综上,点P的坐标为:∴P(﹣3,0)或(0,3![]() )或(0,﹣
)或(0,﹣![]() )或(1,0)或(3+2
)或(1,0)或(3+2![]() ,0)或(3﹣2
,0)或(3﹣2![]() ,0).
,0).
证明:P5(3+2![]() ,0),
,0),
∵∠OAD=30°且△ADO是直角三角形,
又∵AO=3,DO=![]() ,
,
∴DA=2![]() ,
,
而P5A=|3+2![]() ﹣3|=2
﹣3|=2![]() ,
,
∴P5A=DA,
∴△P5AD是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA与x轴重合,B的坐标为(﹣1,2),将矩形OABC绕平面内一点P顺时针旋转90°,使A、C两点恰好落在反比例函数![]() 的图象上,则旋转中心P点的坐标是( )
的图象上,则旋转中心P点的坐标是( )

A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为任意实数,随着k的变化,抛物线y=x2﹣2(k﹣1)x+k2﹣3的顶点随之运动,则顶点运动时经过的路径与两条坐标轴围成图形的面积是( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
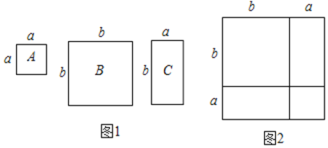
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1:______;方法2:______.
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.______;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(a+b)(a+2b)=a2+3ab+2b2
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x-2016)2+(x-2018)2=34,求(x-2017)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是在写字台上放置一本摊开的数学书和一个折叠式台灯时的截面示意图,已知摊开的数学书AB长20cm,台灯上半节DE长40cm,下半节DC长50cm.当台灯灯泡E恰好在数学书AB的中点O的正上方时,台灯上、下半节的夹角即∠EDC=120°,下半节DC与写字台FG的夹角即∠DCG=75°,求BC的长.(书的厚度和台灯底座的宽度、高度都忽略不计,F、A、O、B、C、G在同一条直线上.参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.41,结果精确到0.1)
≈1.41,结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=3,AD=6,点E是边AD上的一个动点,把△BAE沿BE折叠,若点A的对应点A′恰落在矩形ABCD的对称轴上,则AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王某月手机话费中的各项费用统计情况如图表所示,请你根据图表信息完成下列各题
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 4.8 | 48 |
|
|

(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com