
【题目】数学活动
问题情境:
如图1,在ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将ADE绕点A顺时针旋转α角(0°<α<90°)得到AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
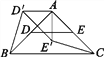 图1
图1 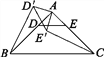 图2
图2 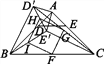 图3
图3 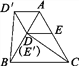 图4
图4
探究发现:
(1)图1中,CE′与BD′的数量关系是________;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E”,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在(2)的条件下,连接BE′,CD′,分别取BC,CD′,E′D′,BE′的中点F,G,H,I,顺次连接F,G,H,I得到四边形FGHI.请判断四边形FGHI的形状,并说明理由;
(4)如图4,在ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将ADE绕点A顺时针旋转60°得到AD′E′,连接CE′,BD′.请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
【答案】CE′=BD′
【解析】试题分析:(1)先证明AD=AE,再根据旋转得到∠BAD′=∠CAE′=α,AD′=AE′,证明△ABD′≌△ACE′,根据全等三角形的对应边相等即可得;
(2)类比(1)的方法先证明AD=AE,然后再证明△ABD′≌△ACE′,根据全等三角形的性质即可得;
(3)先证明四边形FGHI是平行四边形,再证明四边形FGHI是菱形, 延长CE交BD′于点M,由(2)得△ABD′≌△ACE′, 从而推导可得∠CBM+∠BCM=90°,进而可推导得到∠IFG=90°,从而得四边形FGHI是正方形;
(4)答案不唯一,只要符合题意即可.
试题解析:(1) ∵D、E分别为AB、AC的中点,∴AD=![]() AB,AE=
AB,AE=![]() AC,
AC,
∵AB=AC,∴AD=AE,
∵△ADE绕点A顺时针旋转α角(0°<α<90°),得到△AD′E′,
∴∠BAD′=∠CAE′=α,AD′=AE′,
在△ABD′和△ACE′中 ,
,
∴△ABD′≌△ACE′,
∴CE′=BD′,
故答案为:CE′=BD′;
(2)CE′与BD′的数量关系还成立,理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB.
∴∠ADE=∠AED,∴ AD=AE,
∵△ADE绕点A顺时针旋转α角(0°<α<90°),得到△AD′E′,
∴∠BAD′=∠CAE′=α,AD′=AE′,
在△ABD′和△ACE′中 ,
,
∴ △ABD′≌△ACE′,
∴ CE′=BD′;
(3)四边形FGHI是正方形,
∵F,G,H,I分别是BC,CD′,E′D′,BE′的中点,
∴FG=HI=![]() BD′,IF=HG=
BD′,IF=HG=![]() CE′.
CE′.
∴四边形FGHI是平行四边形,
又∵BD′=CE′,∴FG=IF,
∴四边形FGHI是菱形,
延长CE交BD‘于点M,如图,
由(2)得△ABD′≌△ACE′,
∴∠ACE′=∠ABD′,
∵∠BAC=90°,
∴∠ACE′+∠ABC+∠BCM=90°,
∴∠ABD′+∠ABC+∠BCM=90°,
∴∠CBM+∠BCM=90°,
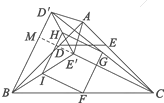
又∵FG∥BD′,IF∥CE′,
∴∠CFG=∠CBM,∠BFI=∠BCM,
∴∠CFG+∠BFI=90°,∴∠IFG=90°,
∴四边形FGHI是正方形;
(4)答案不唯一,如:①△ABD′和△ACE′全等吗?
②△BDD′和△CEE′全等吗?
③∠BD′D和∠CE′E相等吗?
④四边形AD′DE是菱形吗?,


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】元旦是公历新一年的第一天.“元旦”一词最早出现于《晋书》:“颛帝以孟夏正月为元,其实正朔元旦之春.”中国古代曾以腊月、十月等的月首为元旦,1949年中华人民共和国以公历1月1日为元旦,因此元旦在中国也被称为“阳历年”.为庆祝元旦,太原某商场举行促销活动,促销的方法是“消费超过200元时,所购买的商品按原价打8折后,再减少20元”.若某商品的原价为![]() 元,则购买该商品实际付款的金额是( )
元,则购买该商品实际付款的金额是( )
A.![]() 元B.
元B.![]() 元C.
元C.![]() 元D.
元D.![]() 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;
③可能是长方形;④可能是梯形.
其中正确结论的是______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读思考:
数学课上老师出了一道分式化简求值题目.
题目:![]() ÷(x+1)·
÷(x+1)·![]() -
-![]() ,其中x=-
,其中x=-![]() .
.
“勤奋”小组的杨明同学展示了他的解法:
解:原式=![]() -
-![]() ..................第一步
..................第一步
=![]() -
-![]() ................ ..第二步
................ ..第二步
=![]() ..........................第三步
..........................第三步
=![]() ..................................第四步
..................................第四步
当x=-![]() 时,原式=
时,原式= .......................第五步
.......................第五步
请你认真阅读上述解题过程,并回答问题:
你认为该同学的解法正确吗?如有错误,请指出错误在第几步,并写出完整、正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示是一枚质地均匀的骰子.骰子有六个面并分别代表数字1,2,3,4,5,6.如图2,正六边形ABCDEF的顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子向上的一面上的点数是几,就沿正六边形的边顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从圈D开始顺时针连续跳2个边长,落到圈F……
设游戏者从圈A起跳.
(1)小明随机掷一次骰子,求落回到圈A的概率P1;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈A的概率P2,并指出他与小明落回到圈A的可能性一样吗?
 图1
图1 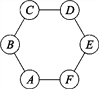 图2
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个无理数筛选器的工作流程图.

(1)当![]() 时,
时,![]() 的值为_____________;
的值为_____________;
(2)是否存在输入有意义的![]() 的值后,却输不出
的值后,却输不出![]() 的值?如果存在,写出所有满足要求的
的值?如果存在,写出所有满足要求的![]() 的值;如果不存在,请说明理由;
的值;如果不存在,请说明理由;
(3)当输出的![]() 的值是
的值是![]() 时,判断输入的
时,判断输入的![]() 的值是否唯一,如果不唯一,请写出其中的
的值是否唯一,如果不唯一,请写出其中的![]() 个.
个.
查看答案和解析>>
科目:初中数学 来源: 题型:
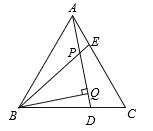
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
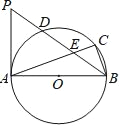
【题目】如图,AB是⊙O的直径,BC为弦,D为弧AC的中点,AC、BD相交于点E.AP交BD的延长线于点P.∠PAC=2∠CBD.
(1)求证:AP是⊙O的切线;
(2)若PD=3,AE=5,求△APE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
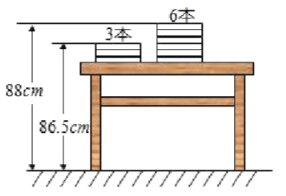
【题目】如图,两摞规格完全相同的课本整齐叠放在桌子上,请根据图中所给出的数据信息,回答下列问题:
(1)每本课本的厚度为 ![]() ;
;
(2)若有一摞上述规格的课本![]() 本,整齐叠放在桌子上,请用含
本,整齐叠放在桌子上,请用含![]() 的代数式表示出这一摞数学课本的顶部距离地面的高度为( )
的代数式表示出这一摞数学课本的顶部距离地面的高度为( )![]() ;
;
(3)当![]() 时,若从中取走15本,求余下的课本的顶部距离地面的高度.
时,若从中取走15本,求余下的课本的顶部距离地面的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com