练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

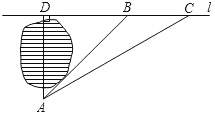
    【题目】如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路．现新修一条路AC到公路l．小明测量出∠ACD=31°，∠ABD=45°，BC=100m．请你帮小明计算他家到公路l的距离AD的长度？(精确到1m；参考数据tan31°≈0.60，sin31°≈0.51，cos31°≈0.86)．

    【答案】小明家到公路l的距离AD的长度约为150m．

    【解析】

    先根据∠ABD=45°得出，然后设AD=BD=x m，利用tan31°即可求出x的值，则答案可求．

    ∵∠ABD=45°，

    设AD=BD=x m，

    ∵∠ACD=31°，BC=100m，

    ∴tan31°0.60，

    解得x=150，

    ∴他家到公路l的距离AD的长度约为150m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】抛物线：与轴交于，两点．（点在点的左侧）

    （1）①填空：时，点的坐标　 　，点的坐标　 　；当时，点的坐标　 　，点的坐标　 　．

    ②猜想：随值的变化，抛物线是否会经过某一个定点，若会，请求出该定点的坐标：若不会，请说明理由．

    （2）若将抛物线经过适当平移后，得到抛物线：，，的对应点分别为，，求抛物线的解析式．

    （3）设抛物线的顶点为，当为直角三角形时，求方程的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，用长33米的竹篱笆围成一个矩形院墙，其中一面靠墙，墙长15米，墙的对面有一个2米宽的门，设垂直于墙的一边长为米，院墙的面积为平方米．

    （1）直接写出与的函数关系式；

    （2）若院墙的面积为143平方米，求的值；

    （3）若在墙的对面再开一个宽为米的门，且面积的最大值为165平方米，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，CD是弦，且CD⊥AB于点P，若AB＝4，OP＝1，则弦CD所对的圆周角等于_____度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

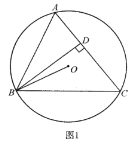
    【题目】内接于边于点，连接．

    如图1，求证:；

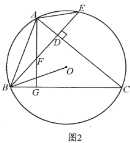
    如图2，延长交于点，点在线段上，射线交边于点，连接，若，求证:；

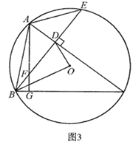
    如图3，在的条件下，连接，若，，求线段的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，若二次函数y=ax2+bx+c（a≠0）图象的对称轴为x=1，与y轴交于点C，与x轴交于点A、点B（﹣1，0），则

    ①二次函数的最大值为a+b+c；

    ②a﹣b+c＜0；

    ③b2﹣4ac＜0；

    ④当y＞0时，﹣1＜x＜3，其中正确的个数是（　　）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P，Q分别是AD和AE上的动点，则DQ＋PQ的最小值是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，AD平分∠CAB交BC于D点，O是AB上一点，经过A、D两点的⊙O分别交AB、AC于点E、F．

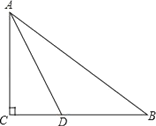
    （1）用尺规补全图形（保留作图痕迹，不写作法）；

    （2）求证：BC与⊙O相切；

    （3）当AD=2，∠CAD=30°时，求劣弧AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】材料1：在设计人体雕塑时，存在一个分隔点，使雕塑的上部（腰以上）与下部（腰以下）之比，等于下部与全部（全身）之比，可以增加视觉美观，数学上把这个点叫“黄金分割点”． 为了研究这个点，我们在线段AB上取点C（如图1），点C把AB分成AC和CB两段，其中BC是较小的一段，现要使即可．为了简便起见，设AB=1，AC=x，则CB=1-x，代入，即，也即x2+x-1=0，解之得，．所以=，人们把这个数叫黄金分割数，点C叫“黄金分割点”．

    材料2：由线段的黄金分割点联想到图形的“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分（设S1＜S2），如果，那么称直线l为该图形的“黄金分割线”．

    （1）如图2，点C是线段AB的黄金分割点（AC>CB），取线段AB的中点O，作点C关于点O的对称点，则；继续取线段AC的中点，作点关于点的对称点，试猜想点是否线段A的黄金分割点，若是，请证明，若不是，请说明理由；

    （2）如图3，在平面直角坐标系中， A（-，0），B（1，0），C（4-，2），求△ABC中经过点C的“黄金分割线”解析式．

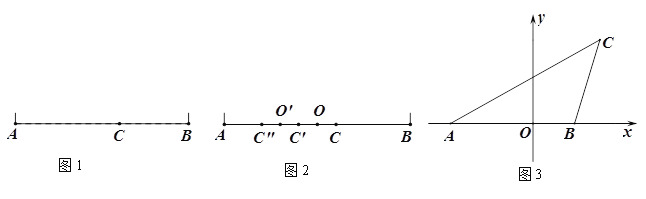
    查看答案和解析>>

    同步练习册答案