
【题目】材料1:在设计人体雕塑时,存在一个分隔点,使雕塑的上部(腰以上)与下部(腰以下)之比,等于下部与全部(全身)之比,可以增加视觉美观,数学上把这个点叫“黄金分割点”. 为了研究这个点,我们在线段AB上取点C(如图1),点C把AB分成AC和CB两段,其中BC是较小的一段,现要使![]() 即可.为了简便起见,设AB=1,AC=x,则CB=1-x,代入
即可.为了简便起见,设AB=1,AC=x,则CB=1-x,代入![]() ,即
,即![]() ,也即x2+x-1=0,解之得,
,也即x2+x-1=0,解之得,![]() .所以
.所以![]() =
=![]() ,人们把
,人们把![]() 这个数叫黄金分割数,点C叫“黄金分割点”.
这个数叫黄金分割数,点C叫“黄金分割点”.
材料2:由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果![]() ,那么称直线l为该图形的“黄金分割线”.
,那么称直线l为该图形的“黄金分割线”.
(1)如图2,点C是线段AB的黄金分割点(AC>CB),取线段AB的中点O,作点C关于点O的对称点![]() ,则
,则![]() ;继续取线段AC的中点
;继续取线段AC的中点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,试猜想点
,试猜想点![]() 是否线段A
是否线段A![]() 的黄金分割点,若是,请证明,若不是,请说明理由;
的黄金分割点,若是,请证明,若不是,请说明理由;
(2)如图3,在平面直角坐标系中, A(-![]() ,0),B(1,0),C(4-
,0),B(1,0),C(4-![]() ,2),求△ABC中经过点C的“黄金分割线”解析式.
,2),求△ABC中经过点C的“黄金分割线”解析式.
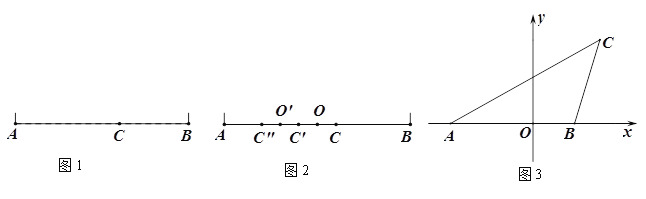
【答案】(1)![]() ,点
,点![]() 是线段A
是线段A![]() 的黄金分割点,理由详见解析;(2)
的黄金分割点,理由详见解析;(2)![]()
【解析】
(1)![]()
![]() ,根据中点及对称点的性质得到A
,根据中点及对称点的性质得到A![]() =BC,再根据线段成比例证得点
=BC,再根据线段成比例证得点![]() 是否线段A
是否线段A![]() 的黄金分割点;
的黄金分割点;
(2)过点C作CH⊥x轴于点H,分两种情况:①当![]() >
>![]() 时,②当
时,②当![]() <
<![]() 时,分别证明点D是线段AB的黄金分割点,由此求出解析式.
时,分别证明点D是线段AB的黄金分割点,由此求出解析式.
(1)![]()
点![]() 是线段A
是线段A![]() 的黄金分割点,理由如下:
的黄金分割点,理由如下:
∵OC=O![]() ,
,
∴AO - O![]() =BO-OC,
=BO-OC,
∴A![]() =BC,
=BC,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴点![]() 是AC的黄金分割点,
是AC的黄金分割点,
∴![]() ,
,
同理可得
![]()
∴![]()
∴![]() 是线段A
是线段A![]() 的黄金分割点
的黄金分割点
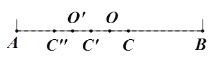
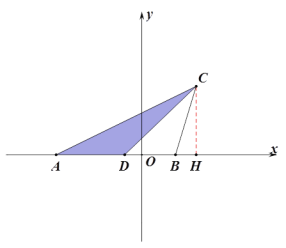
(2)设直线CD是△ABC的黄金分割线,点D的坐标为(x,0),直线CD的解析式为:![]() ,
,
过点C作CH⊥x轴于点H,
![]() ,
,![]() ,
,![]() ,
,
①当![]() >
>![]() 时,
时,
∵直线CD是△ABC的黄金分割线,
∴![]() ,
,
∴![]() ,
,
∴点D是线段AB的黄金分割点,
∴![]() =
=![]() ,
,![]() ,
,
解之得,x=2-![]() ,
,
∵直线![]() 经过D(2-
经过D(2-![]() ,0),C(4-
,0),C(4-![]() ,2),
,2),
∴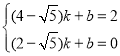 ,
,
解之得,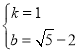 ,
,
∴![]() ;
;
②当![]() <
<![]() 时,
时,
∵直线CD是△ABC的黄金分割线,
∴![]() ,
,
∴![]() ,
,
∴点D是线段AB的黄金分割点,
∴![]() =
=![]() ,
,![]() =,
=,![]()
解之得,![]() ,
,
∵直线![]() 经过C(4-
经过C(4-![]() ,2),D(-1,0),
,2),D(-1,0),
∴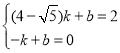 ,
,
解之得,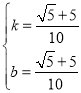 ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
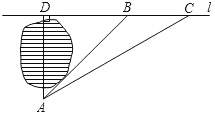
【题目】如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=100m.请你帮小明计算他家到公路l的距离AD的长度?(精确到1m;参考数据tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
请结合上述材料,解决下列问题:
(1)M{(﹣2)2,22,﹣22}=_____;
(2)若min{3﹣2x,1+3x,﹣5}=﹣5,则x的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有3个相同的小球,将3个小球分别标示号码1、2、3,每次从盒子里随机取出1个小球且取后放回,预计取球10次.若规定每次取球时,取出的号码即为得分,则前八次的取球得分情况如下表所示
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 |
(1)设第1次至第8次取球得分的平均数为![]() ,求
,求![]() 的值:
的值:
(2)求事件“第9次和第10次取球得分的平均数等于![]() ”发生的概率;(列表法或树状图)
”发生的概率;(列表法或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 两个口袋,
两个口袋,![]() 口袋中装有两个分别标有数字2,3的小球,
口袋中装有两个分别标有数字2,3的小球,![]() 口袋中装有三个分别标有数字
口袋中装有三个分别标有数字![]() 的小球(每个小球质量、大小、材质均相同).小明先从
的小球(每个小球质量、大小、材质均相同).小明先从![]() 口袋中随机取出一个小球,用
口袋中随机取出一个小球,用![]() 表示所取球上的数字;再从
表示所取球上的数字;再从![]() 口袋中顺次取出两个小球,用
口袋中顺次取出两个小球,用![]() 表示所取两个小球上的数字之和.
表示所取两个小球上的数字之和.
(1)用树状图法或列表法表示小明所取出的三个小球的所有可能结果;
(2)求![]() 的值是整数的概率.
的值是整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
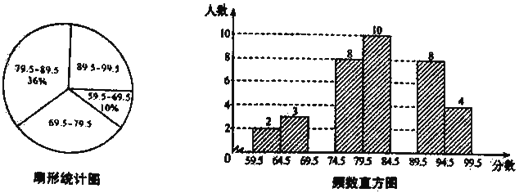
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011广西崇左,18,3分)已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( )

A. ①⑤ B. ①②⑤ C. ②⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若整数a使关于x的分式方程![]() 的解为整数,且使关于y的不等式组
的解为整数,且使关于y的不等式组![]() 有解,且最多有4个整数解,则符合条件的所有整数a的和为( )
有解,且最多有4个整数解,则符合条件的所有整数a的和为( )
A.﹣3B.﹣8C.﹣13D.﹣17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com