
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
请结合上述材料,解决下列问题:
(1)M{(﹣2)2,22,﹣22}=_____;
(2)若min{3﹣2x,1+3x,﹣5}=﹣5,则x的取值范围为_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,用长33米的竹篱笆围成一个矩形院墙,其中一面靠墙,墙长15米,墙的对面有一个2米宽的门,设垂直于墙的一边长为![]() 米,院墙的面积为
米,院墙的面积为![]() 平方米.
平方米.

(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若院墙的面积为143平方米,求![]() 的值;
的值;
(3)若在墙的对面再开一个宽为![]() 米的门,且面积
米的门,且面积![]() 的最大值为165平方米,求
的最大值为165平方米,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
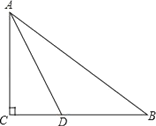
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD=2![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD.

(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,A点的坐标为(﹣3,0),B点在原点的左侧,与y轴交于点C(0,3),点P是直线BC上方的抛物线上一动点
(1)求这个二次函数的表达式;
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C(如图1所示),那么是否存在点P,使四边形POP′C为菱形?若存在,请此时点P的坐标:若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABCP的面积最大,并求出其最大值.
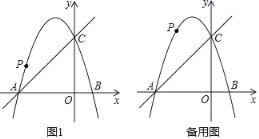
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 内接于⊙
内接于⊙![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() ,满足
,满足![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() ,点
,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() ,
,![]() =
=![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,分别连接
上一点,分别连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交⊙
,交⊙![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
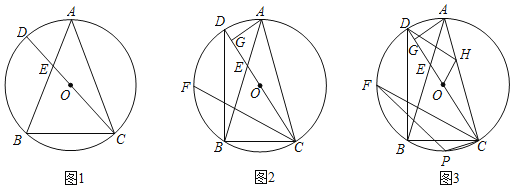
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:在设计人体雕塑时,存在一个分隔点,使雕塑的上部(腰以上)与下部(腰以下)之比,等于下部与全部(全身)之比,可以增加视觉美观,数学上把这个点叫“黄金分割点”. 为了研究这个点,我们在线段AB上取点C(如图1),点C把AB分成AC和CB两段,其中BC是较小的一段,现要使![]() 即可.为了简便起见,设AB=1,AC=x,则CB=1-x,代入
即可.为了简便起见,设AB=1,AC=x,则CB=1-x,代入![]() ,即
,即![]() ,也即x2+x-1=0,解之得,
,也即x2+x-1=0,解之得,![]() .所以
.所以![]() =
=![]() ,人们把
,人们把![]() 这个数叫黄金分割数,点C叫“黄金分割点”.
这个数叫黄金分割数,点C叫“黄金分割点”.
材料2:由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果![]() ,那么称直线l为该图形的“黄金分割线”.
,那么称直线l为该图形的“黄金分割线”.
(1)如图2,点C是线段AB的黄金分割点(AC>CB),取线段AB的中点O,作点C关于点O的对称点![]() ,则
,则![]() ;继续取线段AC的中点
;继续取线段AC的中点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,试猜想点
,试猜想点![]() 是否线段A
是否线段A![]() 的黄金分割点,若是,请证明,若不是,请说明理由;
的黄金分割点,若是,请证明,若不是,请说明理由;
(2)如图3,在平面直角坐标系中, A(-![]() ,0),B(1,0),C(4-
,0),B(1,0),C(4-![]() ,2),求△ABC中经过点C的“黄金分割线”解析式.
,2),求△ABC中经过点C的“黄金分割线”解析式.
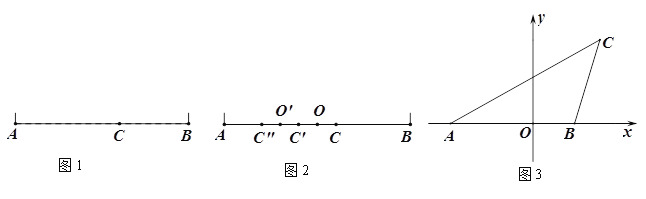
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC.
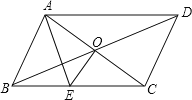
(1)若△ABE的周长为10cm,求平行四边形ABCD的周长;
(2)若∠ABC=78°,AE平分∠BAC,试求∠DAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com