
【题目】已知:![]() 内接于⊙
内接于⊙![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() ,满足
,满足![]() .
.
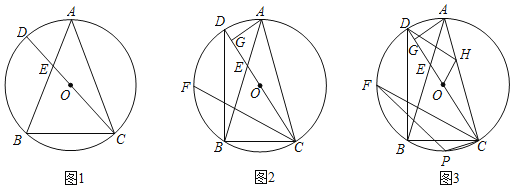
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() ,点
,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() ,
,![]() =
=![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,分别连接
上一点,分别连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交⊙
,交⊙![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)如图1中,连接AD.设∠BEC=3α,∠ACD=α,再根据圆周角定理以及三角形内角和与外角的性质证明∠ACB=∠ABC即可解决问题;
(2)如图2中,连接AD,在CD上取一点Z,使得CZ=BD.证明△ADB≌△AZC(SAS),推出AD=AZ即可解决问题;
(3)连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T.假设OH=![]() a,PC=2a,求出sin∠OHK=
a,PC=2a,求出sin∠OHK=![]() ,从而得出∠OHK=45°,再根据角度的转化得出∠DAG=∠ACO=∠OAK,从而有tan∠ACD=tan∠DAG=tan∠OAK=
,从而得出∠OHK=45°,再根据角度的转化得出∠DAG=∠ACO=∠OAK,从而有tan∠ACD=tan∠DAG=tan∠OAK=![]() ,进而可求出DG,AG的长,再通过勾股定理以及解直角三角形函数可求出FT,PT的长即可解决问题.
,进而可求出DG,AG的长,再通过勾股定理以及解直角三角形函数可求出FT,PT的长即可解决问题.
(1)证明:如图1中,连接AD.设∠BEC=3α,∠ACD=α.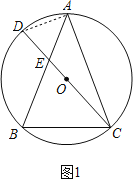
∵∠BEC=∠BAC+∠ACD,
∴∠BAC=2α,
∵CD是直径,
∴∠DAC=90°,
∴∠D=90°-α,
∴∠B=∠D=90°-α,
∵∠ACB=180°-∠BAC-∠ABC=180°-2α-(90°-α)=90°-α.
∴∠ABC=∠ACB,
∴AB=AC.
(2)证明:如图2中,连接AD,在CD上取一点Z,使得CZ=BD.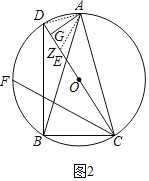
∵![]() =
=![]() ,
,
∴DB=CF,
∵∠DBA=∠DCA,CZ=BD,AB=AC,
∴△ADB≌△AZC(SAS),
∴AD=AZ,
∵AG⊥DZ,
∴DG=GZ,
∴CG=CZ+GZ=BD+DG=CF+DG.
(3)解:连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T.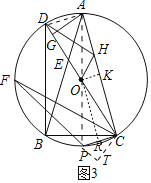
∵CP⊥AC,
∴∠ACP=90°,
∴PA是直径,
∵OR⊥PC,OK⊥AC,
∴PR=RC,∠ORC=∠OKC=∠ACP=90°,
∴四边形OKCR是矩形,
∴RC=OK,
∵OH:PC=1:![]() ,
,
∴可以假设OH=![]() a,PC=2a,
a,PC=2a,
∴PR=RC=a,
∴RC=OK=a,sin∠OHK=![]() ,
,
∴∠OHK=45°.
∵OH⊥DH,
∴∠DHO=90°,
∴∠DHA=180°-90°-45°=45°,
∵CD是直径,
∴∠DAC=90°,
∴∠ADH=90°-45°=45°,
∴∠DHA=∠ADH,
∴AD=AH,
∵∠COP=∠AOD,
∴AD=PC,
∴AH=AD=PC=2a,
∴AK=AH+HK=2a+a=3a,
在Rt△AOK中,tan∠OAK=![]() ,OA=
,OA=![]() ,
,
∴sin∠OAK=![]() ,
,
∵∠ADG+∠DAG=90°,∠ACD+∠ADG=90°,
∴∠DAG=∠ACD,
∵AO=CO,
∴∠OAK=∠ACO,
∴∠DAG=∠ACO=∠OAK,
∴tan∠ACD=tan∠DAG=tan∠OAK=![]() ,
,
∴AG=3DG,CG=3AG,
∴CG=9DG,
由(2)可知,CG=DG+CF,
∴DG+12=9DG,
∴DG=![]() ,AG=3DG=3×
,AG=3DG=3×![]() =
=![]() ,
,
∴AD=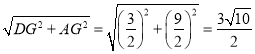 ,
,
∴PC=AD=![]() .
.
∵sin∠F=sin∠OAK,
∴sin∠F=![]() ,
,
∴CT=![]() ,
,
FT=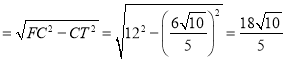 ,
,
PT=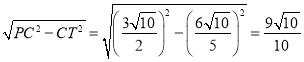 ,
,
∴PF=FT-PT=![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对“隔离直线”给出如下定义:点
中,对“隔离直线”给出如下定义:点![]() 是图形
是图形![]() 上的任意一点,点
上的任意一点,点![]() 是图形
是图形![]() 上的任意一点,若存在直线
上的任意一点,若存在直线![]() :
:![]() 满足
满足![]() 且
且![]() ,则称直线
,则称直线![]() :
:![]() 是图形
是图形![]() 与
与![]() 的“隔离直线”,如图
的“隔离直线”,如图![]() ,直线
,直线![]() :
:![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的一条“隔离直线”.
的一条“隔离直线”.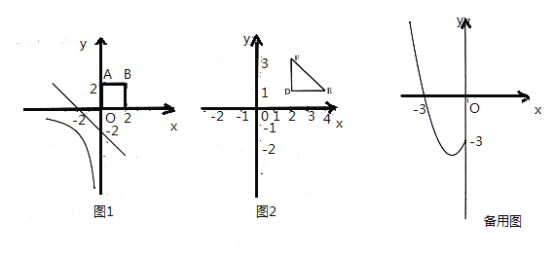
(1)在直线①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,是图
中,是图![]() 函数
函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”的为 .
的“隔离直线”的为 .
(2)如图![]() ,第一象限的等腰直角三角形
,第一象限的等腰直角三角形![]() 的两腰分别与坐标轴平行,直角顶点
的两腰分别与坐标轴平行,直角顶点![]() 的坐标是
的坐标是![]() ,⊙O的半径为
,⊙O的半径为![]() ,是否存在
,是否存在![]() 与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
(3)正方形![]() 的一边在
的一边在![]() 轴上,其它三边都在
轴上,其它三边都在![]() 轴的左侧,点
轴的左侧,点![]() 是此正方形的中心,若存在直线
是此正方形的中心,若存在直线![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”,请直接写出
的“隔离直线”,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
请结合上述材料,解决下列问题:
(1)M{(﹣2)2,22,﹣22}=_____;
(2)若min{3﹣2x,1+3x,﹣5}=﹣5,则x的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有3个相同的小球,将3个小球分别标示号码1、2、3,每次从盒子里随机取出1个小球且取后放回,预计取球10次.若规定每次取球时,取出的号码即为得分,则前八次的取球得分情况如下表所示
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 |
(1)设第1次至第8次取球得分的平均数为![]() ,求
,求![]() 的值:
的值:
(2)求事件“第9次和第10次取球得分的平均数等于![]() ”发生的概率;(列表法或树状图)
”发生的概率;(列表法或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 两个口袋,
两个口袋,![]() 口袋中装有两个分别标有数字2,3的小球,
口袋中装有两个分别标有数字2,3的小球,![]() 口袋中装有三个分别标有数字
口袋中装有三个分别标有数字![]() 的小球(每个小球质量、大小、材质均相同).小明先从
的小球(每个小球质量、大小、材质均相同).小明先从![]() 口袋中随机取出一个小球,用
口袋中随机取出一个小球,用![]() 表示所取球上的数字;再从
表示所取球上的数字;再从![]() 口袋中顺次取出两个小球,用
口袋中顺次取出两个小球,用![]() 表示所取两个小球上的数字之和.
表示所取两个小球上的数字之和.
(1)用树状图法或列表法表示小明所取出的三个小球的所有可能结果;
(2)求![]() 的值是整数的概率.
的值是整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011广西崇左,18,3分)已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( )

A. ①⑤ B. ①②⑤ C. ②⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com