
����Ŀ��һ����������3����ͬ��С��3��С��ֱ��ʾ����1��2��3��ÿ�δӺ��������ȡ��1��С����ȡ��Żأ�Ԥ��ȡ��10�Σ����涨ÿ��ȡ��ʱ��ȡ���ĺ��뼴Ϊ�÷֣���ǰ�˴ε�ȡ��÷�������±���ʾ
���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�÷� | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 |
��1�����1������8��ȡ��÷ֵ�ƽ����Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��2�����¼�����9�κ͵�10��ȡ��÷ֵ�ƽ��������![]() �������ĸ��ʣ����б�������״ͼ��
�������ĸ��ʣ����б�������״ͼ��
���𰸡���1��2����2���б���������![]()
��������
��1������ƽ�����ļ��㷽�����м��㼴�ɣ�
��2�����б����оٳ����еȿ��ܳ��ֵ�����������ҳ����������������������������ʣ�
��1��![]() ����2+1+1+2+2+3+2+3����8��2��
����2+1+1+2+2+3+2+3����8��2��
��2���ñ����г����п��ܳ��ֵ�������£�
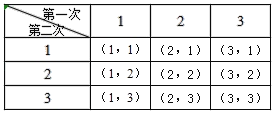
������9�κ͵�10��ȡ��÷ֵ�ƽ��������![]() ��Ҳ�������γ�������ĺ�Ϊ4��
��Ҳ�������γ�������ĺ�Ϊ4��
����9����������к�Ϊ4����3�֣�
��P�����η��ĺ�Ϊ4����![]() ��
��![]() ��
��
���¼�����9�κ͵�10��ȡ��÷ֵ�ƽ��������![]() �������ĸ���Ϊ
�������ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CD���ң���CD��AB�ڵ�P����AB��4��OP��1������CD���Ե�Բ�ܽǵ���_____�ȣ�
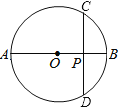
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����ADƽ�֡�CAB��BC��D�㣬O��AB��һ�㣬����A��D����ġ�O�ֱ�AB��AC�ڵ�E��F��
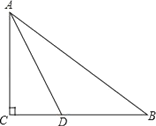
��1���ó߹油ȫͼ�Σ�������ͼ�ۼ�����д��������
��2����֤��BC���O���У�
��3����AD=2![]() ����CAD=30��ʱ�����ӻ�AD�ij���
����CAD=30��ʱ�����ӻ�AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
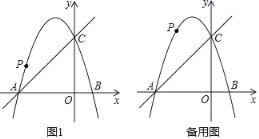
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y����x2+bx+c��ͼ����x�ύ��A��B���㣬A�������Ϊ����3��0����B����ԭ�����࣬��y�ύ�ڵ�C��0��3������P��ֱ��BC�Ϸ�����������һ����
��1����������κ����ı���ʽ��
��2������PO��PC�����ѡ�POC��CO���ۣ��õ��ı���POP��C����ͼ1��ʾ������ô�Ƿ���ڵ�P��ʹ�ı���POP��CΪ���Σ������ڣ����ʱ��P�����꣺�������ڣ���˵�����ɣ�
��3������P�˶���ʲôλ��ʱ���ı���ABCP����������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() �ڽ��ڡ�
�ڽ��ڡ�![]() ������
������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ������
������![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
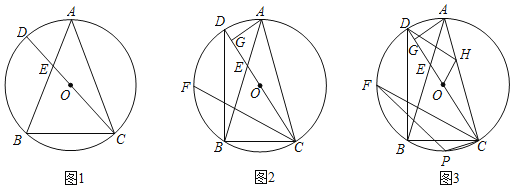
��1����ͼ1����֤��![]() ��
��
��2����ͼ2������![]() ����
����![]() ��
Ϊ��![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() =
=![]() ������
������![]() ��
��![]() ��������
������Ϊ��![]() ����֤��
����֤��![]() ��
��
��3����ͼ3���ڣ�2���������£���![]() Ϊ
Ϊ![]() ��һ�㣬�ֱ�����
��һ�㣬�ֱ�����![]() ��
��![]() ������
������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ������
������![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
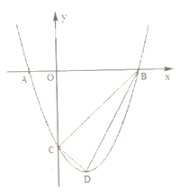
����Ŀ����ͼ��������![]() ���ύ��
���ύ��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���������ߵĶ���Ϊ��
���������ߵĶ���Ϊ��![]() ��
��
��1����������ߵĽ���ʽ�붥��![]() �����꣮
�����꣮
��2�����ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3�����������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() Ϊ�������������
Ϊ�������������![]() ���ƣ������ڣ���ֱ��д����
���ƣ������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1��������������ʱ������һ���ָ��㣬ʹ���ܵ��ϲ��������ϣ����²��������£�֮�ȣ������²���ȫ����ȫ����֮�ȣ����������Ӿ����ۣ���ѧ�ϰ����������ƽ�ָ������ Ϊ���о�����㣬�������߶�AB��ȡ��C����ͼ1������C��AB�ֳ�AC��CB���Σ�����BC�ǽ�С��һ�Σ���Ҫʹ![]() ���ɣ�Ϊ�˼���������AB=1��AC=x����CB=1-x������
���ɣ�Ϊ�˼���������AB=1��AC=x����CB=1-x������![]() ����
����![]() ��Ҳ��x2+x-1=0����֮�ã�
��Ҳ��x2+x-1=0����֮�ã�![]() ������
������![]() =
=![]() �����ǰ�
�����ǰ�![]() ������лƽ�ָ�������C�����ƽ�ָ������
������лƽ�ָ�������C�����ƽ�ָ������
����2�����߶εĻƽ�ָ�����뵽ͼ�ε����ƽ�ָ����������Ƶظ������ƽ�ָ������Ķ��壺ֱ��l��һ�����ΪS��ͼ�ηֳ����ΪS1�����ΪS2�������֣���S1��S2�������![]() ����ô��ֱ��lΪ��ͼ�ε����ƽ�ָ�������
����ô��ֱ��lΪ��ͼ�ε����ƽ�ָ�������
��1����ͼ2����C���߶�AB�Ļƽ�ָ�㣨AC>CB����ȡ�߶�AB���е�O������C���ڵ�O�ĶԳƵ�![]() ����
����![]() ������ȡ�߶�AC���е�
������ȡ�߶�AC���е�![]() ������
������![]() ���ڵ�
���ڵ�![]() �ĶԳƵ�
�ĶԳƵ�![]() ���Բ����
���Բ����![]() �Ƿ��߶�A
�Ƿ��߶�A![]() �Ļƽ�ָ�㣬���ǣ���֤���������ǣ���˵�����ɣ�
�Ļƽ�ָ�㣬���ǣ���֤���������ǣ���˵�����ɣ�
��2����ͼ3����ƽ��ֱ������ϵ�У� A��-![]() ��0����B��1��0����C��4-
��0����B��1��0����C��4-![]() ��2��������ABC�о�����C�����ƽ�ָ���������ʽ��
��2��������ABC�о�����C�����ƽ�ָ���������ʽ��
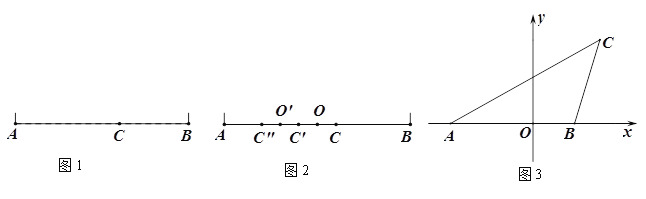
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+bx+4����A����3��0����B��4��0�����㣬����y�ύ�ڵ�C��D��4��4![]() ��0��������P�ӵ�A���������߶�AB��ÿ��1����λ���ȵ��ٶ����B�ƶ���ͬʱ����Q�ӵ�C���������߶�CA��ijһ�ٶ����A�ƶ���
��0��������P�ӵ�A���������߶�AB��ÿ��1����λ���ȵ��ٶ����B�ƶ���ͬʱ����Q�ӵ�C���������߶�CA��ijһ�ٶ����A�ƶ���
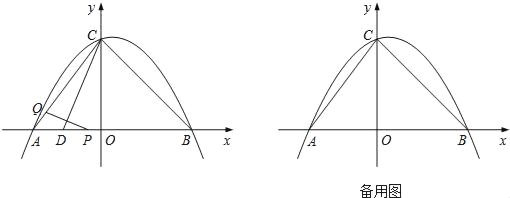
��1����������ߵĽ���ʽ��
��2��������t����ƶ����߶�PQ��CD��ֱƽ�֣����ʱt��ֵ��
��3���ڵ�һ������������ȡһ��G��ʹ��S��GCB��S��GCA���������������ҵ�E�������A��B��C�غϣ���ʹ�á�GBE��45�㣬��E������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABC�У���A��60������C��90��������ABC�Ƶ�B˳ʱ����ת150�����õ���DBE��������̶ȵ�ֱ�ߣ���Ҫ��ͼ��������ͼ�ۼ�����ͼ�б����ĸ������ͼ�·���ʾ������ͼ�Σ���
��1����ͼ���У���һ���ȱ������Σ�
��2����ͼ���У���һ������ֱ�������Σ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com