
【题目】如图,用长33米的竹篱笆围成一个矩形院墙,其中一面靠墙,墙长15米,墙的对面有一个2米宽的门,设垂直于墙的一边长为![]() 米,院墙的面积为
米,院墙的面积为![]() 平方米.
平方米.

(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若院墙的面积为143平方米,求![]() 的值;
的值;
(3)若在墙的对面再开一个宽为![]() 米的门,且面积
米的门,且面积![]() 的最大值为165平方米,求
的最大值为165平方米,求![]() 的值.
的值.
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
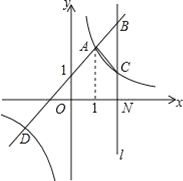
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月17日,我国第一艘国产航母“山东舰”在海南三亚交付海军.如图,“山东舰”在一次试水测试中,航行至![]() 处,观测指挥塔
处,观测指挥塔![]() 位于南偏西
位于南偏西![]() 方向,在沿正南方向以30海里/小时的速度匀速航行2小时后,到达
方向,在沿正南方向以30海里/小时的速度匀速航行2小时后,到达![]() 处,再观测指挥塔
处,再观测指挥塔![]() 位于南偏西
位于南偏西![]() 方向,若继续向南航行.求“山东舰”与指挥塔之间的最近距离为多少海里?(结果保留根号)
方向,若继续向南航行.求“山东舰”与指挥塔之间的最近距离为多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
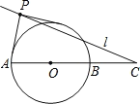
【题目】如图,已知⊙O 的半径长为2,点C为直径AB的延长线上一点,且BC=2.过点C任作一条直线l.若直线l上总存在点P,使得过点P所作的⊙O 的两条切线互相垂直,则∠ACP的最大值等于__________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(1,0),C(0,2).
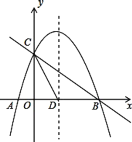
(1)求抛物线的表达式;
(2) 请你在抛物线的对称轴上找点P,使△PCD是以CD为腰的等腰三角形,所有符合条件的点P的坐标分别为 ;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+8与反比例函数![]() (x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于D点.
(x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于D点.
(1)求反比例函数的解析式.
(2)在第一象限内,根据图象直接写出一次函数值大于反比例函数值时自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
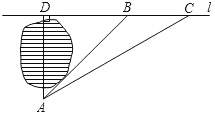
【题目】如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=100m.请你帮小明计算他家到公路l的距离AD的长度?(精确到1m;参考数据tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
请结合上述材料,解决下列问题:
(1)M{(﹣2)2,22,﹣22}=_____;
(2)若min{3﹣2x,1+3x,﹣5}=﹣5,则x的取值范围为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com