练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
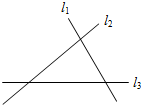
    17．如图所示，直线l1，l2，l3表示三条相交的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（　　）
    A．1处B．2处C．3处D．4处

    分析 根据到三条相互交叉的公路距离相等的地点应是三条角平分线的交点．把三条公路的中心部位看作三角形，那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求．

    解答 解：满足条件的有：
    （1）三角形两个内角平分线的交点，共一处；
    （2）三个外角平分线两两相交的交点，共三处．
    故选：D．

    点评 本题考查了角平分线的性质；这是一道生活联系实际的问题，解答此类题目时最直接的判断就是三角形的角平分线，很容易漏掉外角平分线，解答时一定要注意，不要漏解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．在直角坐标系中，点A、B的坐标分别为（-2，4）、（-5，2），点M是x轴上的点，点N是y轴上的点，如果以点A、B、M、N为顶点的四边形是平行四边形，那么符合条件的点M有（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图是由9个等边三角形拼成的六边形，若已知中间的小等边三角形的边长是2，则六边形的周长是60．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

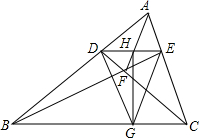    5．在△ABC中，D，E分别为AB，AC上一点，DE交AF于H，HG⊥BC，连接DG，GE．
    （1）证明：GH为△DGE的一条平分线；
    （2）过H的一条直线交DF，AE分别于M，N，证明：GH为△MNG的一条角平分线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

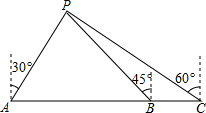    12．天宜号船向正东方航行（如图），船在A处时测得灯塔在P北偏东30°方向，前进到B处时测得灯塔P恰好在西北方向，又航行半小时到达C处，此时测得灯塔P在北偏西60°方向，若船速为每小时20海里，求A、C两点间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．x2-2x-1=0，则$\frac{x^2}{{{x^4}+{x^2}+1}}$=$\frac{1}{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．若关于x的方程$\frac{2x-b}{x-1}=1$的解是非负数，则b的取值范围是b≥1且b≠2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在梯形ABCD中，AD∥BC，AB⊥BC，E是CD的中点，F在AB上，且∠1=∠2，AE、DF交于P，BE、CF交于Q，求证：四边形EPFQ是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列分式中，最简分式是（　　）
    A．$\frac{1-x}{2（x+1）}$B．$\frac{x-2y}{{x}^{2}-4{y}^{2}}$C．$\frac{x+1}{2{x}^{2}+4x+2}$D．$\frac{x+3{x}^{2}}{{x}^{2}}$

    查看答案和解析>>

    同步练习册答案