
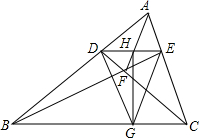
 在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE.
在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE.分析 (1)首先延长ED与CB的延长线交于K,利用梅涅劳斯定理以及塞瓦定理得出$\frac{DK}{KE}$=$\frac{DH}{HE}$,进而由调和点列结论1得,GH平分∠DGE,求出即可;
(2)首先延长NM交BC于S,连接AM并延长,交BC于T,梅涅劳斯定理以及塞瓦定理得出$\frac{MS}{SN}$=$\frac{MH}{HN}$,进而由调和点列结论1得,GH平分∠MGN,求出即可.
解答 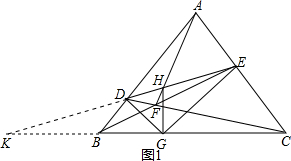 证明:(1)延长ED与CB的延长线交于K,
证明:(1)延长ED与CB的延长线交于K,
对于直线CBK截得△ADE,由梅涅劳斯定理得:
$\frac{AB}{BD}$•$\frac{DK}{KE}$•$\frac{EC}{CA}$=1①,
对于点F与△ADE,由塞瓦定理得:
$\frac{AB}{BD}$•$\frac{DH}{HE}$•$\frac{EC}{CA}$=1②,
①=②得:$\frac{DK}{KE}$=$\frac{DH}{HE}$,
∴线段DE被点H、K调和,
∵∠KGH=90°,
由调和点列结论1得,GH平分∠DGE,
即GH为△DGE的一条平分线;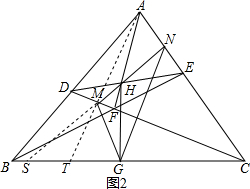
(2)延长NM交BC于S,连接AM并延长,交BC于T,对于直线STC截得△AMN,
由梅涅劳斯定理得:$\frac{AT}{TM}$•$\frac{MS}{SN}$•$\frac{NC}{CA}$=1①,
对于点F与△AME,由塞瓦定理得:
$\frac{AT}{TM}$•$\frac{NH}{HN}$•$\frac{NC}{CA}$=1②,
①=②得,$\frac{MS}{SN}$=$\frac{MH}{HN}$,
∴线段MN被点H、S调和,
∵∠KGH=90°,
由调和点列结论1得,GH平分∠MGN,
即GH为△MNG的一条角平分线.
点评 此题主要考查了梅涅劳斯定理与赛瓦定理,根据题意正确应用梅涅劳斯定理与赛瓦定理得出正确等量关系是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{13}{7}$ | B. | $\frac{7}{13}$ | C. | -$\frac{2009}{7}$ | D. | -$\frac{2009}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
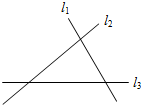 如图所示,直线l1,l2,l3表示三条相交的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图所示,直线l1,l2,l3表示三条相交的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )| A. | 1处 | B. | 2处 | C. | 3处 | D. | 4处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
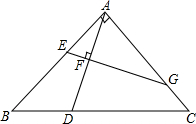 如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.
如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com