
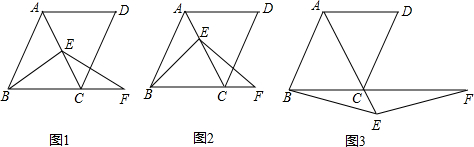
分析 (1)根据菱形的性质证明△ABC是等边三角形和AB=2,求出△ABC的面积;
(2)作EG∥BC交AB于G,证明△BGE≌△ECF,得到BE=EF;
(3)作EH∥BC交AB的延长线于H,证明△BHE≌△ECF,得到BE=EF.
解答 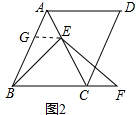 解:(1)∵四边形ABCD是菱形,∠ABC=60°,
解:(1)∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,又E是线段AC的中点,
∴BE⊥AC,AE=$\frac{1}{2}$AB=1,
∴BE=$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$×AC×BE=$\sqrt{3}$;
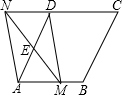
(2)如图2,作EG∥BC交AB于G,
∵△ABC是等边三角形,
∴△AGE是等边三角形,
∴BG=CE,
∵EG∥BC,∠ABC=60°,
∴∠BGE=120°,
∵∠ACB=60°,
∴∠ECF=120°,
∴∠BGE=∠ECF,
在△BGE和△ECF中,
$\left\{\begin{array}{l}{GE=CF}\\{∠BGE=∠ECF}\\{BG=CE}\end{array}\right.$,
∴△BGE≌△ECF,
∴EB=EF;
(3)成立,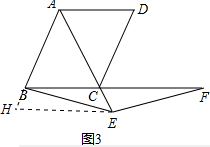 如图3,作EH∥BC交AB的延长线于H,
如图3,作EH∥BC交AB的延长线于H,
∵△ABC是等边三角形,
∴△AHE是等边三角形,
∴BH=CE,
在△BHE和△ECF中,
$\left\{\begin{array}{l}{BH=CE}\\{∠BHE=∠ECF}\\{HE=CF}\end{array}\right.$,
∴△BHE≌△ECF,
∴EB=EF.
点评 本题考查的是菱形的性质、等边三角形的性质、全等三角形的判定和性质,正确作出辅助线、灵活运用相关的判定定理和性质定理是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
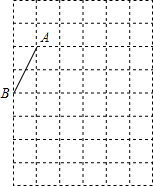 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,骑自行车和步行的速度始终保持不变,则小明在比赛开始前5分钟到达体育馆.
某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,骑自行车和步行的速度始终保持不变,则小明在比赛开始前5分钟到达体育馆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)商店有A、B、C、D四种饮料,每种饮料数量充足,某同学去该店购买饮量,每种饮料被选中的可能性相同.
(1)商店有A、B、C、D四种饮料,每种饮料数量充足,某同学去该店购买饮量,每种饮料被选中的可能性相同.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2xy-7=0 | B. | $\sqrt{2}$x2-7=0 | C. | $\frac{1}{{x}^{2}}$-7x=0 | D. | 5(x+1)=72 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com