
【题目】在平面直角坐标系中,我们不妨把横坐标和纵坐标都是整数的点称为“中国结”.直线![]() 与
与![]()
![]() 交于一点.
交于一点.
(1)求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)如图,定点![]() ,动点
,动点![]() 在直线
在直线![]() 上运动.当线段
上运动.当线段![]() 最短时,求出点
最短时,求出点![]() 的坐标,并判断点
的坐标,并判断点![]() 是否为“中国结”;
是否为“中国结”;
(3)当直线![]() 与
与![]() 的交点为“中国结”时,求满足条件的
的交点为“中国结”时,求满足条件的![]() 值.
值.

【答案】(1)(-1,0);(2)见解析;(3) 0, 2 ,3, 5, -1,-3.
【解析】
(1)令y=0即可求出直线与x轴的交点坐标;(2)当线段AB最短时,AB垂直直线y=x-3,可设直线AB的解析式为:y=-x+b,把A点代入即可求出B点坐标,即可判断;(3)联立直线![]() 与
与![]() ,再求出整点坐标对应的k值即可.
,再求出整点坐标对应的k值即可.
(1)令y=0,kx+k=0,则x=-1
∴直线与x轴的交点坐标(-1,0)
(2)当线段AB最短时,AB垂直直线y=x-3
∴设直线AB的解析式为:y=-x+b
∴0=5+b b=-5
所以直线AB的解析式为:y=-x-5
解![]() 得
得![]()
∴B(-1,-4),B点为中国结
(3)由题意得:
![]() 解得:
解得: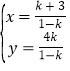
所以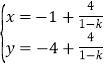
∵交点为整数,
∴k可取的整数解有0, 2 ,3, 5, -1,-3共6个


科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() EC,其中正确结论的序号是______.
EC,其中正确结论的序号是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,点D,E分别在直线AB,BC上,且∠DEC=∠DCE.
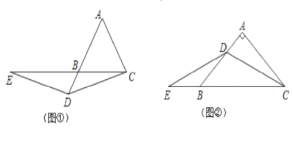
(1)如图①,若点D在线段AB的延长线上,∠A=60°,求证:EB=AD;
(2)如图②,若点D在线段AB上,∠A=90°,求证:EB=![]() AD;
AD;
(3)在(2)的条件下,若CD平分∠ACB,P是线段CD上任意一点,点Q,P关于BC对称,且BE=2,请直接写出△BPQ周长的最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠AOD交CD于E,OF⊥EO,OG⊥CD,∠D=50°,则下列结论:①∠AOE=60°;②∠DOF=25°;③∠GOE=∠DOF;④OF平分∠BOD,其中正确的个数是( )
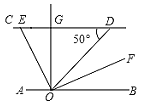
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直角坐标系中直线 AB 与 x 轴正半轴、y 轴正半轴交于 A,B 两点,已知 B(0,4),∠BAO=30°,P,Q 分别是线段 OB,AB 上的两个动点,P 从 O 出发以每秒 3 个单位长度的速度向终点 B 运动,Q 从 B 出发以每秒 8 个单位长度的速度向终点 A 运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为 t(秒).
(1)求线段 AB 的长,及点 A 的坐标;
(2)t 为何值时,△BPQ 的面积为![]() ;
;
(3)若 C 为 OA 的中点,连接 QC,QP,以 QC,QP 为邻边作平行四边形 PQCD,
①t 为何值时,点 D 恰好落在坐标轴上;
②是否存在时间 t 使 x 轴恰好将平行四边形 PQCD 的面积分成 1∶3 的两部分,若存在,直接写出 t 的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com