
分析 (1)根据函数y=x+$\frac{a}{x}$(a>0,x>0),当x=$\sqrt{a}$时,该函数有最小值为2$\sqrt{a}$,得到当x=$\sqrt{9}$=3时,y1+y2取得最小值为2$\sqrt{9}$=6,
(2)由$\frac{{y}_{2}}{{y}_{1}}$=$\frac{{(x+1)}^{2}+4}{x+1}$=(x+1)+$\frac{4}{x+1}$,得到当x+1=$\sqrt{4}$=2,即:x=1时,$\frac{y2}{y1}$的最小值=2$\sqrt{4}$=4;
(3)根据耗油总量=每公里的耗油量×行驶的速度列出函数关系式即可,经济时速就是耗油量最小的形式速度.
解答 解:(1)∵对于函数y=x+$\frac{a}{x}$(a>0,x>0),当x=$\sqrt{a}$时,该函数有最小值为2$\sqrt{a}$,
∴当x=$\sqrt{9}$=3时,y1+y2取得最小值为2$\sqrt{9}$=6,
(2)∵$\frac{{y}_{2}}{{y}_{1}}$=$\frac{{(x+1)}^{2}+4}{x+1}$=(x+1)+$\frac{4}{x+1}$,
∴当x+1=$\sqrt{4}$=2,即:x=1时,$\frac{y2}{y1}$的最小值=2$\sqrt{4}$=4;
(3)∵汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油($\frac{1}{18}$+$\frac{450}{{x}^{2}}$)升.
∴y=x×($\frac{1}{18}$+$\frac{450}{{x}^{2}}$)=$\frac{x}{18}$+$\frac{450}{x}$,(70≤x≤110);
根据材料得:当$\frac{x}{18}$=$\frac{450}{x}$时有最小值,
解得:x=90
∴该汽车的经济时速为90千米/小时;
当x=90时百公里耗油量为100×($\frac{1}{18}$+$\frac{450}{8100}$)≈11.1升.
点评 本题考查了反比例函数的应用,最值问题,解题的关键是读懂题目提供的材料,易错点是了解“耗油总量=每公里的耗油量×行驶的速度”,难度中等偏上.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
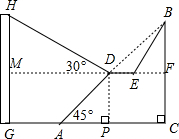 市政府对城市建设进行了整改,如图,已知斜坡AB长90$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(后两个小题结果都保留根号).
市政府对城市建设进行了整改,如图,已知斜坡AB长90$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(后两个小题结果都保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{10}$,4 | B. | 2$\sqrt{10}$,4 | C. | 4,3$\sqrt{2}$ | D. | 6$\sqrt{2}$,4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com