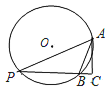
【题目】如图，
的半径为2，弦
，点P为优弧AB上一动点，
，交直线PB于点C，则
的最大面积是
A.
B.1C.2D.
科目：初中数学 来源： 题型：
【题目】在一个不透明的口袋里装有分别标有数字﹣3、﹣1、0、2的四个小球，除数字不同外，小球没有任何区别，每次实验先搅拌均匀．
(1)从中任取一球，求抽取的数字为正数的概率；
(2)从中任取一球，将球上的数字记为a，求关于x的一元二次方程ax2﹣2ax+a+3＝0有实数根的概率；
(3)从中任取一球，将球上的数字作为点的横坐标，记为x(不放回)；再任取一球，将球上的数字作为点的纵坐标，记为y，试用画树状图(或列表法)表示出点(x，y)所有可能出现的结果，并求点(x，y)落在第二象限内的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
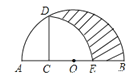
【题目】如图，AB为半圆O的直径，C为AO的中点，CD⊥AB交半圆于点D，以C为圆心，CD为半径画弧DE交AB于E点，若AB=4cm，则图中阴影部分的面积为__________cm2.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图 (1)，已知△ABC是等边三角形，以BC为直径的⊙O交AB、AC于D、E.求证：
(1)△DOE是等边三角形.
(2)如图(2)，若∠A=60°，AB≠AC， 则(1)中结论是否成立？如果成立，请给出证明；如果不成立，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ACB＝90°，sinA＝
，BC＝8，点D是AB的中点，过点B作CD的垂线，垂足为点E.
(1)求线段CD的长；
(2)求cos∠ABE的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．
（1）若∠AOD=52°，求∠DEB的度数；
（2）若OC=3，OA=5，求AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论：①abc＜0；②2a+b＝0； ③b2﹣4ac＜0； ④9a+3b+c＞0.其中正确的结论有____________（ 填序号 ）
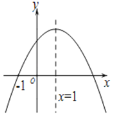
查看答案和解析>>
科目：初中数学 来源： 题型：
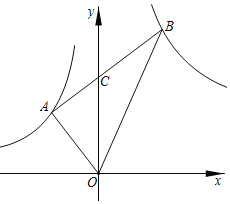
【题目】如图，Rt△AOB中，∠OAB＝90°，∠OBA＝30°，顶点A在反比例函数y＝
图象上，若Rt△AOB的面积恰好被y轴平分，则进过点B的反比例函数的解析式为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，△ABC为等边三角形，其中点A、B、C的坐标分别为（﹣3，﹣1）、（﹣3，﹣3）、（﹣3+
，﹣2）．现以y轴为对称轴作△ABC的对称图形，得△A1B1C1，再以x轴为对称轴作△A1B1C1的对称图形，得△A2B2C2．
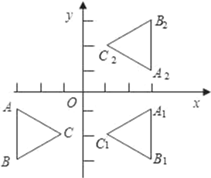
①直接写出点C1的坐标 ，点C2的坐标 ；
②能否通过一次旋转将△ABC旋转到△A2B2C2的位置？你若认为能，请作出肯定的回答，并直接写出所旋转的度数；你若认为不能，请作出否定的回答（不必说明理由）；
③设当△ABC的位置发生变化时，△A2B2C2、△A1B1C1、△ABC之间的对称关系始终保持不变，当△ABC向上平移多少个单位时，△A1B1C1与△A2B2C2完全重合？并直接写出此时点C的坐标？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
