
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

科目:初中数学 来源: 题型:
【题目】某种速冻水饺的储藏温度是﹣18±2℃,四个冷藏室的温度如下,则不适合储藏此种水饺的是( )
A. ﹣17℃ B. ﹣18℃ C. ﹣19℃ D. ﹣22℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AOB是一条直线,∠AOC=60°,OD,OE分别是∠AOC和∠BOC的平分线,则图中互补的角有( ) 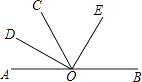
A.5对
B.6对
C.7对
D.8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB于点H. 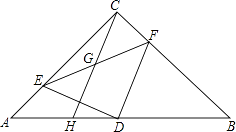
(1)若E在边AC上. ①试说明DE=DF;
②试说明CG=GH;
(2)若AE=3,CH=5.求边AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是(只填写序号). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com