
【题目】若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )
A.1:2
B.2:1
C.1:4
D.4:1
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)、D(2, n)三点.
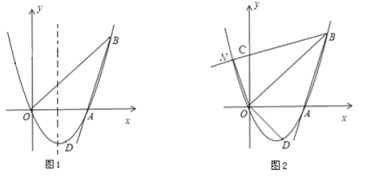
(1)求抛物线的解析式及点D坐标;
(2)点M是抛物线对称轴上一动点,求使BM-AM的值最大时的点M的坐标;
(3)如图2,将射线BA沿BO翻折,交y轴于点C,交抛物线于点N,求点N的坐标;
(4)在(3)的条件下,连结ON,OD,如图2,请求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出;怎样计算1×2+2×3+3×4+…+(n﹣1)×n呢?
材料学习
计算1+2+3…+n
因为1= ![]() (1×2﹣0×1);2=
(1×2﹣0×1);2= ![]() (2×3﹣1×2);3=
(2×3﹣1×2);3= ![]() (3×4﹣2×3)
(3×4﹣2×3)
…,n= ![]() [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
所以1+2+3+…+n
= ![]() (1×2﹣0×1)+
(1×2﹣0×1)+ ![]() (2×3﹣1×2)+
(2×3﹣1×2)+ ![]() (3×4﹣2×3)+…+
(3×4﹣2×3)+…+ ![]() [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
= ![]() [1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]=
[1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]= ![]() n(n+1)
n(n+1)
(1)探究应用
观察规律:①1×2= ![]() (1×2×3﹣0×12);②2×3=
(1×2×3﹣0×12);②2×3= ![]() (2×3×4﹣1×2×3);
(2×3×4﹣1×2×3);
③3×4= ![]() (3×4×5﹣2×3×4);…
(3×4×5﹣2×3×4);…
猜想归纳:
根据(1)中观察的规律直接写出:4×5= ![]() ()
()
(n﹣1)×n= ![]() []
[]
问题解决:
1×2+2×3+3×4+4×5…+(n﹣1)×n
= ![]() (1×2×3﹣0×1×2)+
(1×2×3﹣0×1×2)+ ![]() (2×3×4﹣1×2×3)+
(2×3×4﹣1×2×3)+ ![]() (3×4×5﹣2×3×4)+…+
(3×4×5﹣2×3×4)+…+ ![]() []
[]
=
(2)拓展延伸
根据上面的规律,请直接写出1×2×3+2×3×4+3×4×5+…+(n﹣2)(n﹣1)n= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为进行危房改造,政府最近将在某校搭建板房,从某厂调拔了用于搭建板房的板材5600m3和铝材2210m3 , 计划用这些材料在某校搭建甲、乙两种规格的板房共100间.若搭建一间甲型 板房或一间乙型板房所需板材和铝材的数量如表所示:
板房规格 | 板材数量(m3) | 铝材数量(m3) |
甲型 | 40 | 30 |
乙型 | 60 | 20 |
请你根据以上信息,设计出甲、乙两种板房的搭建方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点. 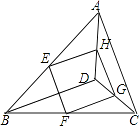
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com