
【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)、D(2, n)三点.
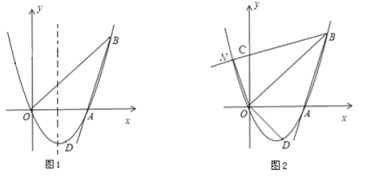
(1)求抛物线的解析式及点D坐标;
(2)点M是抛物线对称轴上一动点,求使BM-AM的值最大时的点M的坐标;
(3)如图2,将射线BA沿BO翻折,交y轴于点C,交抛物线于点N,求点N的坐标;
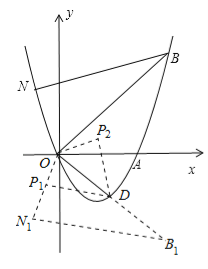
(4)在(3)的条件下,连结ON,OD,如图2,请求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
【答案】(1)y=x2﹣3x;(2,﹣2);(2)(![]() ,);(3)(
,);(3)(![]() );(4)(
);(4)(![]() )或(
)或(![]() ).
).
【解析】
试题分析:(1)根据曲线上点的坐标与方程的关系,将(3,0)、B(4,4)代入y=ax2+bx即可求得抛物线的解析式,令x=2,即可求得点D坐标;
(2)抛物线对称轴上使BM-AM的值最大时的点M即直线AB与抛物线对称轴的交点,从而应用待定系数法求出直线AB的解析式,即可求得点M的坐标;
(3)用待定系数法求出直线CB的解析式,由点N在直线CB和抛物线y=x2﹣3x上,即可求出N点的坐标;
(4)应用对称或旋转的性质即可求得点P的坐标.
试题解析:(1)∵抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4),
∴抛物线的解析式是y=x2﹣3x.∴D点的坐标为(2,﹣2).
(2)设直线AB解析式为:y=kx+m, 将 A(3,0)、B(4,4)代人得
![]() ,解得
,解得![]() . ∴直线AB解析式为:
. ∴直线AB解析式为:![]() .
.
∵抛物线对称轴为![]() ,当
,当![]() 时,
时,![]() ,
,
∴当点M(![]() ,)时,BM-AM的值最大.
,)时,BM-AM的值最大.
(3)∵直线OB的解析式为y=x,且A(3,0),
根据轴对称性质得出∠CBO=∠ABO,∠COB=∠AOB,OB=OB, ∴△AOB≌△COB.
∴OC=OA. ∴点C(0,3).
设直线CB的解析式为y=kx+3,过点(4,4),∴直线CB的解析式是![]() .
.
∵点N在直线CB上,∴设点N(n,![]() ).
).
又点N在抛物线y=x2﹣3x上,∴![]() ,解得:n1=
,解得:n1=![]() ,n2=4(不合题意,舍去)。
,n2=4(不合题意,舍去)。
∴N点的坐标为(![]() ).
).
(4)如图,将△NOB沿x轴翻折,得到△N1OB1,则N1(![]() ),B1(4,﹣4),
),B1(4,﹣4),
∴O、D、B1都在直线y=﹣x上.
∵△P1OD∽△NOB,△NOB≌△N1OB1,∴△P1OD∽△N1OB1. ∴![]() .
.
∴点P1的坐标为(![]() ).
).
将△OP1D沿直线y=﹣x翻折,可得另一个满足条件的点P2(![]() ).
).
综上所述,点P的坐标是(![]() )或(
)或(![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列从左到右的变形,属于因式分解的是( )
A.(x+3)(x﹣2)=x2+x﹣6
B.ax﹣ay﹣1=a(x﹣y)﹣1
C.8a2b3=2a24b3
D.x2﹣4=(x+2)(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两边长分别为方程x2﹣8x+15=0的两根,则该三角形周长L的取值范围是( )
A. 6<L<15B. 6<L<16C. 10<L<16D. 11<L<13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD;这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有( )
A. 3种 B 4种 C 5种 D 6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
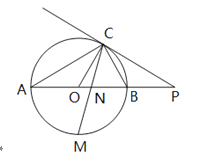
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四边形的三个内角的度数依次如下,那么其中是平行四边形的是( )
A. 88°,108°,88° B. 88°,104°,88°
C. 88°,92°,92° D. 88°,92°,88°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com