
【题目】问题提出;怎样计算1×2+2×3+3×4+…+(n﹣1)×n呢?
材料学习
计算1+2+3…+n
因为1= ![]() (1×2﹣0×1);2=
(1×2﹣0×1);2= ![]() (2×3﹣1×2);3=
(2×3﹣1×2);3= ![]() (3×4﹣2×3)
(3×4﹣2×3)
…,n= ![]() [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
所以1+2+3+…+n
= ![]() (1×2﹣0×1)+
(1×2﹣0×1)+ ![]() (2×3﹣1×2)+
(2×3﹣1×2)+ ![]() (3×4﹣2×3)+…+
(3×4﹣2×3)+…+ ![]() [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
= ![]() [1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]=
[1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]= ![]() n(n+1)
n(n+1)
(1)探究应用
观察规律:①1×2= ![]() (1×2×3﹣0×12);②2×3=
(1×2×3﹣0×12);②2×3= ![]() (2×3×4﹣1×2×3);
(2×3×4﹣1×2×3);
③3×4= ![]() (3×4×5﹣2×3×4);…
(3×4×5﹣2×3×4);…
猜想归纳:
根据(1)中观察的规律直接写出:4×5= ![]() ()
()
(n﹣1)×n= ![]() []
[]
问题解决:
1×2+2×3+3×4+4×5…+(n﹣1)×n
= ![]() (1×2×3﹣0×1×2)+
(1×2×3﹣0×1×2)+ ![]() (2×3×4﹣1×2×3)+
(2×3×4﹣1×2×3)+ ![]() (3×4×5﹣2×3×4)+…+
(3×4×5﹣2×3×4)+…+ ![]() []
[]
=
(2)拓展延伸
根据上面的规律,请直接写出1×2×3+2×3×4+3×4×5+…+(n﹣2)(n﹣1)n= .
【答案】
(1)4×5×6﹣3×4×5;(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n;(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n;![]() [1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]=
[1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]= ![]() (n﹣1)n(n+1)
(n﹣1)n(n+1)![]()
(2)![]()
(n﹣2)(n﹣1)n(n+1)
【解析】解:(1)4×5= ![]() (4×5×6﹣3×4×5);
(4×5×6﹣3×4×5);
1×2+2×3+3×4+4×5…+(n﹣1)×n
= ![]() (1×2×3﹣0×1×2)+
(1×2×3﹣0×1×2)+ ![]() (2×3×4﹣1×2×3)+
(2×3×4﹣1×2×3)+ ![]() (3×4×5﹣2×3×4)+…+
(3×4×5﹣2×3×4)+…+ ![]() [(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]
[(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]
= ![]() [1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]
[1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]
= ![]() (n﹣1)n(n+1);
(n﹣1)n(n+1);
2)问题解决:1×2×3+2×3×4+3×4×5+…+(n﹣2)(n﹣1)n
= ![]() (1×2×3×4﹣0×1×2×3)+
(1×2×3×4﹣0×1×2×3)+ ![]() (2×3×4×5﹣1×2×3×4)+
(2×3×4×5﹣1×2×3×4)+ ![]() (3×4×5×6﹣2×3×4×5)+…+
(3×4×5×6﹣2×3×4×5)+…+ ![]() [(n﹣2)(n﹣1)n(n+1)﹣(n﹣3)(n﹣2)(n﹣1)n]
[(n﹣2)(n﹣1)n(n+1)﹣(n﹣3)(n﹣2)(n﹣1)n]
= ![]() [1×2×3×4﹣0×1×2×3+2×3×4×5﹣1×2×3×4+3×4×5×6﹣2×3×4×5+…+(n﹣2)(n﹣1)n(n+1)﹣(n﹣3)(n﹣2)(n﹣1)n]
[1×2×3×4﹣0×1×2×3+2×3×4×5﹣1×2×3×4+3×4×5×6﹣2×3×4×5+…+(n﹣2)(n﹣1)n(n+1)﹣(n﹣3)(n﹣2)(n﹣1)n]
= ![]() (n﹣2)(n﹣1)n(n+1).
(n﹣2)(n﹣1)n(n+1).
所以答案是:4×5×6﹣3×4×5,(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n;(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n,= ![]() [1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n],
[1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n], ![]() (n﹣1)n(n+1);
(n﹣1)n(n+1); ![]() (n﹣2)(n﹣1)n(n+1).
(n﹣2)(n﹣1)n(n+1).
【考点精析】掌握有理数的四则混合运算是解答本题的根本,需要知道在没有括号的不同级运算中,先算乘方再算乘除,最后算加减.


科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
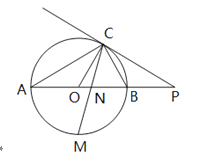
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四边形的三个内角的度数依次如下,那么其中是平行四边形的是( )
A. 88°,108°,88° B. 88°,104°,88°
C. 88°,92°,92° D. 88°,92°,88°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种速冻水饺的储藏温度是﹣18±2℃,四个冷藏室的温度如下,则不适合储藏此种水饺的是( )
A. ﹣17℃ B. ﹣18℃ C. ﹣19℃ D. ﹣22℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AOB是一条直线,∠AOC=60°,OD,OE分别是∠AOC和∠BOC的平分线,则图中互补的角有( ) 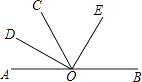
A.5对
B.6对
C.7对
D.8对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com