
����Ŀ����ͼ����֪��ABC�У���B=��C��AB=AC=12cm��BC=8cm����DΪAB���е��������P���߶�BC����2cm/s���ٶ���B����C���˶���ͬʱ����Q���߶�CA������C��A���˶���

��1������Q���˶��ٶ����P���˶��ٶ���ȣ�����1�����BPD����CQP�Ƿ�ȫ��?��˵��������
��2������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD����CQPȫ�ȣ�
���𰸡���1����BPD�ա�CPQ�����ɼ���������2��3��
��������
�����������1���������⣬���BP��CQ��CP�ij�������SAS�����ж���BPD�ա�CQP����2����֪��Q���˶��ٶ����P���˶��ٶȲ���ȣ��ɵ�BP��CQ��������BPD����CPQȫ�ȣ���B=��C�ɵ�BP=PC=4cm��CQ=BD=6cm���ɴ˿ɵõ�P��Q���˶�ʱ����
�����������1����BPD�ա�CPQ��
����������t=1����
��BP=CQ=2��1=2������
��AB=12���ף���DΪAB���е㣬
��BD=6������
����PC=BC��BP��BC=8���ף�
��PC=8��2=6���ף�
��PC=BD��
����AB=AC��
���B=��C��
����BPD����CPQ��

���BPD�ա�CQP
��2������Q���˶��ٶ����P���˶��ٶȲ���ȣ�
��BP��CQ��
���ߡ�BPD����CPQȫ�ȣ���B=��C��
��BP=PC=4cm��CQ=BD=6cm��
����P����Q�˶���ʱ��Ϊ4��2=2�룬
��Q����˶��ٶ�Ϊ6��2=3����/�룻


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ס��������ֱ�����480km��A��B����������У��ҳ��ȼ׳��ȳ���1Сʱ�����Ը��Ե��ٶ�������ʻ���׳�����C�غ������°�ԭ·ԭ�ٷ���A�أ��ҳ���B��ֱ��A�أ�����ͬʱ����A�أ��ס�����������Գ����ص�·��y��ǧ�ף���׳��������õ�ʱ��x��Сʱ���Ĺ�ϵ��ͼ2�����ͼ����Ϣ����������⣺
��1���ҳ����ٶ����� ��ǧ��/ʱ���ҳ���ʻ��ʱ��t=�� ��Сʱ��
��2����׳���C�ذ�ԭ·ԭ�ٷ���A�صĹ����У��׳����������ص�·��y����������ʱ��x�ĺ�����ϵʽ��
��3��ֱ��д���׳������ʱ���������80ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
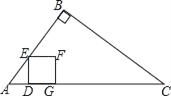
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬AB=6cm��BC=8cm����D�ӵ�A������1cm/s���ٶ��˶�����Cֹͣ����DE��AC����AB��BC�ڵ�E����DEΪ��������������DEFG�����D���˶�ʱ��Ϊt��s����
��1����AC�ij���
��2�����ú�t�Ĵ���ʽ��ʾ�߶�DE�ij���
��3������F�ڱ�BC��ʱ����t��ֵ��
��4����������DEFG����ABC�ص�����ͼ�ε����ΪS��cm2�������ص�����ͼ��Ϊ�ı���ʱ����S��t֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
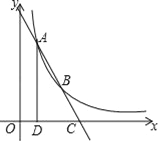
����Ŀ����ͼ����A��1��4����B��2��a���ں���y=![]() ��x��0����ͼ���ϣ�ֱ��AB��x���ཻ�ڵ�C��AD��x���ڵ�D��
��x��0����ͼ���ϣ�ֱ��AB��x���ཻ�ڵ�C��AD��x���ڵ�D��
��1��m=������
��2�����C�����ꣻ
��3����x�����Ƿ���ڵ�E��ʹ��A��B��EΪ���������������ACD���ƣ������ڣ������E�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�����E��F�ֱ��D��C����ͬʱ����������ͬ���ٶ���ֱ��DC��CB���ƶ���
��1����ͼ�٣�����E��D��C����F��C��B�ƶ�ʱ������AE��DF���ڵ�P������д��AE��DF��λ�ù�ϵ����˵�����ɣ�
��2����ͼ�ڣ���E��F�ֱ��ƶ�����DC��CB���ӳ�����ʱ������AE��DF����1���еĽ��ۻ������𣿣�����ֱ�ӻش���������������������֤����
��3����ͼ�ۣ���E��F�ֱ��ڱ�CD��BC���ӳ������ƶ�ʱ������AE��DF����1���еĽ��ۻ���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���O��AC���ϵ�һ�����㣬����O��ֱ��MN��BC����MN����BCA�Ľ�ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F��
��1����֤��EO=FO��
��2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�
��3������O�˶����δ����ҡ�ABC����ʲô����ʱ���ı���AECF�������Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�E��F�ǶԽ���BD�ϵĵ㣬��1=��2.
��֤����1��BE=DF����2��AF��CE.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɳƺ����2017���Ѿ��ɹ�������������������������ȫ������ȫ���������������������������ij�ֵ�������Ӧ�����������Ͷ��һ���ʽ������̻�һ�����ÿյأ������˼ס���������ľ��72�ã����м�����ľÿ��90Ԫ��������ľÿ��80Ԫ������ȥ�ʽ�6160Ԫ.
��1����ס���������ľ�������˶��ٿã�
��2������һ��ʱ�����ֲ��������ľ�ɻ��ʸߣ��̻�Ч���ã��ýֵ������ٹ���һ����������ľ�̻���һ�����ÿյأ�������ľ�Ĺ������������һ����ͬ������ʱ���ּ�����ľ����������![]() ��������ľ�����½���
��������ľ�����½���![]() �����ܷ��ò�����6804Ԫ����
�����ܷ��ò�����6804Ԫ����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��P��������ABCD�ĶԽ���BD��һ��,PE��BC�ڵ�E,PF��CD�ڵ�F,����EF�����������������:��AP=EF����AP��EF���ۡ�APDһ���ǵ��������Σ��ܡ�PFE=��BAP����PD=![]() EC��������ȷ���۵������______.
EC��������ȷ���۵������______.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com