
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;
(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不须证明)
(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;
【答案】(1)AE=DF,AE⊥DF,理由详见解析;(2)是;(3)成立,理由详见解析.
【解析】
(1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;
(2)根据正方形性质得AD=DC,∠ADE=∠DCF=90°,DE=CF,可得△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,故AE⊥DF;
(3)由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF;
(1)AE=DF,AE⊥DF.
理由:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠C=90°.
在△ADE和△DCF中,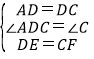 ,
,
∴△ADE≌△DCF(SAS).
∴AE=DF,∠DAE=∠CDF,
由于∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°.
∴AE⊥DF;
(2)是.四边形ABCD是正方形,所以AD=DC,∠ADE=∠DCF=90°,DE=CF,所以△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,所以AE⊥DF;
(3)成立.
理由:由(1)同理可证AE=DF,∠DAE=∠CDF
延长FD交AE于点G,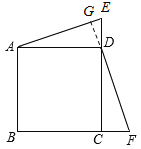
则∠CDF+∠ADG=90°,
∴∠ADG+∠DAE=90°.
∴AE⊥DF;


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,求AD:OC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
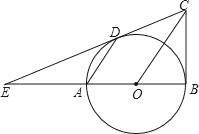
【题目】如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
证明:∵CF⊥AB、DE⊥AB(已知)
∴∠BED=90°、∠BFC=90°
∴∠BED=∠BFC
∴( )∥( )( )
∴∠1=∠BCF( )
又∵∠1=∠2(已知)
∴∠2=∠BCF( )
∴FG∥BC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=∠C,AB=AC=12cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等?请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学习了一元一次方程的解法,下面是林林同学的解题过程:解方程![]() =1
=1
解:方程两边同时乘以6,得:![]() ×6=1×6…………第①步
×6=1×6…………第①步
去分母,得:2(2x+1)-x+2=6………………第②步
去括号,得:4x+2-x+2=6…………………第③步
移项,得:4x-x=6-2-2…………………第④步
合并同类项,得:3x=2…………………………第⑤步
系数化1,得:x=![]() …………………………第⑥步
…………………………第⑥步
上述林林的解题过程从第______步开始出现错误,错误的原因是______.
请你帮林林改正错误,写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复![]() 下表是活动进行中的一组统计数据:
下表是活动进行中的一组统计数据:
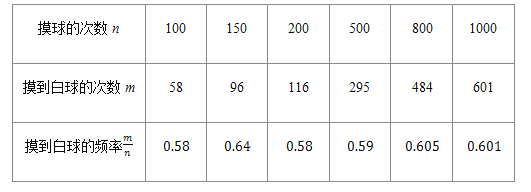
![]() 请估计:当n很大时,摸到白球的频率将会接近______ ;
请估计:当n很大时,摸到白球的频率将会接近______ ;![]() 精确到
精确到![]()
![]() 试估算口袋中白种颜色的球有多少只?
试估算口袋中白种颜色的球有多少只?
![]() 请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如下表:

当n个最小的连续偶数(从2开始)相加时,它们的和与n之间有什么样的关系,请用公式表示出来,并由此计算:
①2+4+6+…+200的值;
②(-22)+(-24)+(-26)+…+(-300)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com