
【题目】如图所示,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,求AD:OC的值.
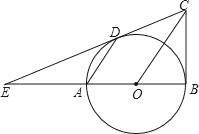
【答案】(1)见解析;(2)2:3
【解析】试题分析:
(1)连接OD,由OD=OA可得∠ODA=∠OAD,由AD∥OC可得:∠OAD=∠COD,∠ODA=∠COD,从而可得∠COD=∠BOC,这样结合OD=OB,OC=OC即可证得△COD≌△COB,由此可得到∠ODC=∠OBC=90°,即可得到直线CD是⊙O的切线;
(2)由△COD≌△COB可得CD=BC结合DE=2BC可得DE=2CD,再证△EAD∽△EOC即可由相似三角形的性质求得AD:OC的比值了.
试题解析:
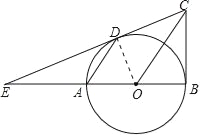
(1)证明:连接OD,
∵OA=OD,
∴∠ODA=∠OAD,
∵AD∥OC,
∴∠OAD=∠COD,∠ODA=∠COD,
∴∠COD=∠BOC,
在△COD和△BOC中: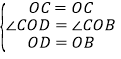 ,
,
∴△COD≌△BOC,
∴∠ODC=∠OBC=90°,
∴CD为圆O的切线;
(2)∵△COD≌△COB,
∴BC=CD,
∵DE=2BC,
∴DE=2CD,
∵AD∥OC,
∴△DAE∽△COE,
∴AD:OC=ED:AC=2:3.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】下列方程的解法中,错误的个数是( )
①方程2x-1=x+1移项,得3x=0
②方程![]() =1去分母,得x-1=3=x=4
=1去分母,得x-1=3=x=4
③方程1-![]() 去分母,得4-x-2=2(x-1)
去分母,得4-x-2=2(x-1)
④方程![]() 去分母,得2x-2+10-5x=1
去分母,得2x-2+10-5x=1
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
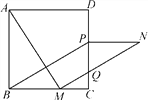
【题目】如图,在正方形ABCD中,点M是BC边上的任一点,连结AM并将线段AM绕点M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连结NP、BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连结AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
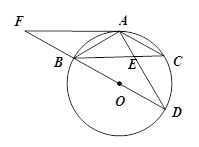
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
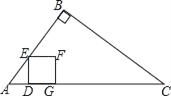
【题目】如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).
(1)求AC的长.
(2)请用含t的代数式表示线段DE的长.
(3)当点F在边BC上时,求t的值.
(4)设正方形DEFG与△ABC重叠部分图形的面积为S(cm2),当重叠部分图形为四边形时,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台2500元、B型每台4000元、C型每台6000元,某中学现有资金100500元,计划全部用于从这家电脑公司购进36台两种型号的电脑这,这个学校有哪几种购买方案可选择,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;
(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不须证明)
(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2﹣7x+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为![]() 时运动时间t的值;
时运动时间t的值;
(3)当点P运动到边AC上时,是否存在点P,使△CDP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com