
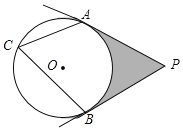
【题目】如图,PA,PB分别与⊙O相切于A,B两点,∠ACB=60°.
(1)求∠P的度数;
(2)若⊙O的半径长为2cm,求图中阴影部分的面积.
【答案】(1)∠P=60°;(2)4![]() -
-![]() π.
π.
【解析】
(1)先证明∠P=180°-∠AOB,根据∠AOB=2∠ACB求出∠AOB即可解决问题.
(2)连接OP,如图,根据切线的性质和切线长定理得到∠PAO=∠PBO=90°,∠APO=30°,则根据四边形内角和得到∠AOB=180°-∠APB=120°,再在Rt△PAO中利用含30度的直角三角形三边的关系得到AP=![]() OA=2
OA=2![]() ,则S△PAO=2
,则S△PAO=2![]() ,然后根据扇形面积公式,利用阴影部分的面积=S四边形AOBP-S扇形AOB进行计算.
,然后根据扇形面积公式,利用阴影部分的面积=S四边形AOBP-S扇形AOB进行计算.
解:(1)连接OA、OB,
∵PA、PB是⊙O切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P+∠PAO+∠AOB+∠PBO=360°,
∴∠P=180°-∠AOB,
∵∠ACB=60°,
∴∠AOB=2∠ACB=120°,
∴∠P=180°-120°=60°,
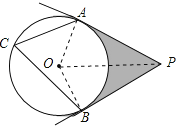
(2)如图,连接OP,
∵PA,PB是⊙O的两条切线,
∴OA⊥AP,OB⊥PB,OP平分∠APB,
∴∠PAO=∠PBO=90°,∠APO=![]() ×60°=30°,
×60°=30°,
∴∠AOB=180°-∠APB=180°-60°=120°,
在Rt△PAO中,∵OA=2,∠APO=30°,
∴AP=![]() OA=2
OA=2![]() ,
,
∴S△PAO=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
∴阴影部分的面积=S四边形AOBP-S扇形AOB=2×2![]() -
-![]() =4
=4![]() -
-![]() π.
π.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 30 | … |
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形的一条边长为x,周长的一半为y,定义(x,y)为这个矩形的坐标。如图2,在平面直角坐标系中,直线x=1,y=3将第一象限划分成4个区域,已知矩形1的坐标的对应点A落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中,则下面叙述中正确的是( )

A. 点A的横坐标有可能大于3
B. 矩形1是正方形时,点A位于区域②
C. 当点A沿双曲线向上移动时,矩形1的面积减小
D. 当点A位于区域①时,矩形1可能和矩形2全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳绳是大家喜闻乐见的一项体育运动,集体跳绳时,需要两人同频甩动绳子,当绳子甩到最高处时,其形状可近似看作抛物线,下图是小明和小亮甩绳子到最高处时的示意图,两人拿绳子的手之间的距离为4![]() ,离地面的高度为1
,离地面的高度为1![]() ,以小明的手所在位置为原点建立平面直角坐标系.
,以小明的手所在位置为原点建立平面直角坐标系.
(1)当身高为15![]() 的小红站在绳子的正下方,且距小明拿绳子手的右侧1
的小红站在绳子的正下方,且距小明拿绳子手的右侧1![]() 处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的表达式;
处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的表达式;
(2)若身高为![]() 的小丽也站在绳子的正下方.
的小丽也站在绳子的正下方.
①当小丽在距小亮拿绳子手的左侧1.5![]() 处时,绳子能碰到小丽的头吗?请说明理由;
处时,绳子能碰到小丽的头吗?请说明理由;
②设小丽与小亮拿绳子手之间的水平距离为![]() ,为保证绳子不碰到小丽的头顶,求
,为保证绳子不碰到小丽的头顶,求![]() 的取值范围.(参考数据:
的取值范围.(参考数据: ![]() 取3.16)
取3.16)

查看答案和解析>>
科目:初中数学 来源: 题型:
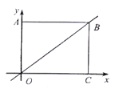
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 分别在坐标轴的正半轴上,
分别在坐标轴的正半轴上, ![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与折线
与折线![]() 有公共点.
有公共点.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)对于一次函数![]() ,当
,当![]() 随
随![]() 的增大而减小时,直接写出
的增大而减小时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
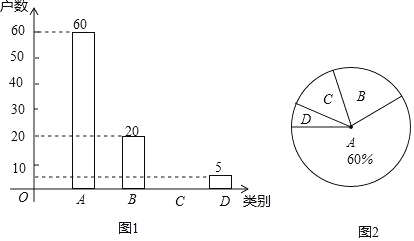
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为3的⊙O经过等边△ABO的顶点A、B,点P为半径OB上的动点,连接AP,过点P作PC⊥AP交⊙O于点C,当∠ACP=30°时,AP的长为( )
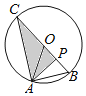
A. 3B. 3或![]() C.
C. ![]() D. 3或
D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
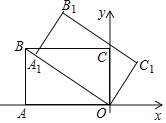
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com