Question

【题目】在平面直角坐标系中，已知M1（3，2），N1（5，－1），线段M1N1平移至线段MN处（注：M1与M，N1与N分别为对应点）.

（1）若M（－2，5），请直接写出N点坐标.

（2）在（1）问的条件下，点N在抛物线上，求该抛物线对应的函数解析式.

（3）在（2）问条件下，若抛物线顶点为B，与y轴交于点A，点E为线段AB中点，点C（0，m）是y轴负半轴上一动点，线段EC与线段BO相交于F，且OC︰OF=2︰，求m的值.

（4）在（3）问条件下，动点P从B点出发，沿x轴正方向匀速运动，点P运动到什么位置时（即BP长为多少），将△ABP沿边PE折叠，△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的，求此时BP的长度.

Answer 1

【答案】（1）N（0,2）；（2）y=x2+ x+2；（3）m=－1；（4）BP=2或

【解析】

（1）首先根据点M的移动方向和单位得到点N的平移方向和单位，然后按照平移方向和单位进行移动即可；（2）将点N的坐标代入函数的解析式即可求得k值；（3）配方后确定点B、A、E的坐标，根据CO：OF=2： 用m表示出线段CO、FO和BF的长，利用S△BEC=S△EBF+S△BFC= S△ABC得到有关m的方程求得m的值即可；（4）分当∠BPE＞∠APE时、当∠BPE=∠APE时、当∠BPE＜∠APE时三种情况分类讨论即可．

（1）N（0,2）

（2）∵N（0,2）在抛物线y=x2+ x+k上

∴k=2

∴抛物线的解析式为y=x2+ x+2

（3）∵y=x2+ x+2=（x+2）2

∴B（－2，0）、A（0,2）、E（－，1）

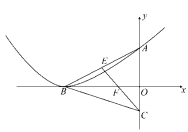
∵CO：OF=2:

∴CO=－m, FO=－m, BF=2+m

∵S△BEC= S△EBF+ S△BFC=

∴(2+m)(－m+1) =

整理得：m2+m = 0

∴m=－1或0

∵m < 0 ∴m =－1

（4）在Rt△ABO中，tan∠ABO===

∴∠ABO=30°，AB=2AO=4

①∠BPE>∠APE时，连接A1B

则对折后如图2，A1为对折后A的所落点，△EHP是重叠部分.

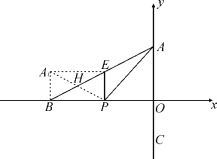
∵E为AB中点，∴S△AEP= S△BEP= S△ABP

∵S△EHP= S△ABP

∴= S△EHP= S△BHP= S△ABP

∴A1H=HP，EH=HB=1

∴四边形A1BPE为平行四边形

∴BP=A1E=AE=2

即BP=2

②当∠BPE=∠APE时，重叠部分面积为△ABP面积的一半，不符合题意

③当∠BPE<∠APE时.

则对折后如图3，A1为对折后A的所落点.△EHP是重叠部分

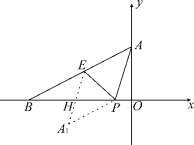
∵E为AB中点，∴S△AEP= S△BEP= S△ABP

∵S△EHP= S△ABP∴S△EBH= S△EHP== S△ABP

∴BH=HP，EH=HA1=1

又∵BE=EA=2

∴EHAP

∴AP=2

在△APB中，∠ABP=30°，AB=4，AP=2.

∴∠APB=90° ∴BP=

综合①②③知：BP=2或