练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．如图，Rt△OAB中，BA⊥OA，且OA=BA=4，点P从O点出发，沿OA以每秒1个单位的速度向A点移动，到达A点停止运动，则△OBP面积S与点P的运动时间t之间的函数图象大致是（　　）
    A．B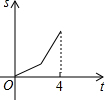．C．D．

    分析 根据点P的运动速度可得出OP=t，再根据三角形的面积公式得出S△OPB=S=$\frac{1}{2}$OP•AB，确定S是t的正比例函数，画出图象即可．

    解答 解：∵OP=t，OA=BA=4，
    ∴S△OPB=S=$\frac{1}{2}$OP•AB=2t，
    ∵P点到达A点停止运动，
    ∴0＜OP＜4，
    ∴S是t的正比例函数，且0＜t＜4．
    故选A．

    点评 本题考查了动点问题的函数图象，以及直角三角形的面积公式，属于综合性的题目，对于此类动点型题目，首先要确定符合题意的条件下动点所在的位置，然后用时间t表示出有关线段的长度，进而建立关于线段的关系式，难度较大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．约分：
    （1）$\frac{（a-x）^{2}}{（x-a）^{3}}$；
    （2）$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知关于x的方程$\frac{m}{{x}^{2}-9}$+$\frac{2}{x+3}$=$\frac{1}{x-3}$无解，求m2+10的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如果（a-b+1）2+$\sqrt{2a-b+4}$=0，求ba的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，把长方形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．
    （1）若∠1=50°，求∠2、∠3的度数；
    （2）若AD=8，AB=4，求BF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某股民上星期五买进某公司股票1000股，每股25元，下表为本周内每日该股票的涨跌情况：（单价：元）
    星期一二三四五
    每股涨跌
    （与前一天比较）    		+2-0.5+1.5-1.8+0.8
    （1）星期三收盘时，每股是多少元？
    （2）本周内最高价是每股多少元？最低价是每股多少元？
    （3）已知该股民买进股票时付了0.15%的手续费，卖出时需付成交额0.15%的手续费和0.1‰的交易税，如果他一直观望到星期五才将股票全部卖出，请算算他本周的收益如何？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图，已知在△ABC中，D是边BC的中点，$\overrightarrow{BA}=\overrightarrow a$，$\overrightarrow{BC}=\overrightarrow b$，那么$\overrightarrow{DA}$等于（　　）
    A．$\frac{1}{2}\overrightarrow a-\overrightarrow b$B．$\overrightarrow a-\frac{1}{2}\overrightarrow b$C．$\frac{1}{2}\overrightarrow b-\overrightarrow a$D．$\overrightarrow b-\frac{1}{2}\overrightarrow a$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，已知AB⊥CD，垂足为B，EF是经过B点的一条直线，∠EBD=145°，则∠ABF的度数为55°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图，在数轴上A、B两点对应的有理数分别是a、b，则下列结论正确的是（　　）
    A．a+b＞0B．|a|＞|b|C．ab＞0D．线段AB的长为a-b

    查看答案和解析>>

    同步练习册答案