练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．如图，已知AB⊥CD，垂足为B，EF是经过B点的一条直线，∠EBD=145°，则∠ABF的度数为55°．

    分析 根据已知条件，利用互补关系，互余关系及对顶角相等的性质解题．

    解答 解：∵∠CBE+∠EBD=180°，∠EBD=145°，
    ∴∠CBE=180°-∠EBD=35°，
    ∵∠CBE与∠DBF是对顶角，
    ∴∠DBF=∠CBE=35°，
    ∵AB⊥CD，
    ∴∠ABF=90°-∠DBF=55°．
    故答案为：55°．

    点评 此题主要考查了角与角的关系，即余角、补角、对顶角的关系，利用互余，互补的定义得出角的度数是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．当x取什么样的值时，下列二次根式有意义？写出简单过程．
    （1）$\sqrt{x-5}$；
    （2）$\sqrt{2-4x}$；
    （3）$\sqrt{\frac{1}{3x+4}}$；
    （4）$\frac{x}{\sqrt{2x-4}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，Rt△OAB中，BA⊥OA，且OA=BA=4，点P从O点出发，沿OA以每秒1个单位的速度向A点移动，到达A点停止运动，则△OBP面积S与点P的运动时间t之间的函数图象大致是（　　）
    A．B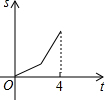．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．点O在直线AB上，点A1，A2，A3，…在射线OA上，点B1，B2，B3，…在射线OB上，图中的每一个实线段和虚线段的长均为1个单位长度．一个动点M从O点出发，以每秒1个单位长度的速度按如图所示的箭头方向沿着实线段和以点O为圆心的半圆匀速运动，即从OA1B1B2→A2…按此规律，则动点M到达A10点处所需时间为（　　）秒．
    A．10+55πB．20+55πC．10+110πD．20+110π

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．将m2（a-2）+m（a-2）分解因式的结果是（　　）
    A．（a-2）（m2-m）B．m（a-2）（m-1）C．m（a-2）（m+1）D．m（2-a）（m-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，P是⊙O外一点，PC为切线，割线PAB经过圆心O．
    （1）若PB=12，PC=4$\sqrt{3}$，求⊙O的半径长；
    （2）作∠BPC的角平分线交BC于D，求∠CDP的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在平面直角坐标系中，直线y=x+3分别交x轴、y轴于A，C两点，抛物线y=ax2+bx+c（a≠0），经过A，C两点，与x轴交于点B（1，0）．
    （1）求抛物线的解析式；
    （2）点D为直线AC上一点，点E为抛物线上一点，且D，E两点的横坐标都为2，点F为x轴上的点，若四边形ADEF是平行四边形，请直接写出点F的坐标；
    （3）若点P是线段AC上的一个动点，过点P作x轴的垂线，交抛物线于点Q，连接AQ，CQ，求△ACQ的面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，在△ABC中，AB=AC，点D在△ABC的外部，∠ACD=∠B，∠ADC=90°．
    （1）作图，作∠BAC的平分线AO，交BC于点O（用尺规作图，保留作图痕迹，不写作法）；
    （2）求证：BC=2CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．若关于y的方程2m+y=1与3y-3=2y-1的解相同，则m的值为（　　）
    A．2B．-$\frac{1}{2}$C．-2D．0

    查看答案和解析>>

    同步练习册答案