
分析 (1)把分子(a-x)2化成(x-a)2,然后再约去分子和分母的公因式,即可得出结果;
(2)首先运用完全平方公式和平方差公式把分子和分母分解因式,然后再约去分子和分母的公因式,即可得出结果.
解答 解:(1)$\frac{(a-x)^{2}}{(x-a)^{3}}$=$\frac{(x-a)^{2}}{(x-a)^{3}}$=$\frac{1}{x-a}$;
(2)$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$=$\frac{(x-1)^{2}}{(x+1)(x-1)}$=$\frac{x-1}{x+1}$.
点评 本题考查了分式的约分、互为相反数的性质、运用完全平方公式和平方差公式分解因式;熟练掌握用完全平方公式和平方差公式分解因式是解决问题的关键.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,Rt△OAB中,BA⊥OA,且OA=BA=4,点P从O点出发,沿OA以每秒1个单位的速度向A点移动,到达A点停止运动,则△OBP面积S与点P的运动时间t之间的函数图象大致是( )
如图,Rt△OAB中,BA⊥OA,且OA=BA=4,点P从O点出发,沿OA以每秒1个单位的速度向A点移动,到达A点停止运动,则△OBP面积S与点P的运动时间t之间的函数图象大致是( )| A. |  | B. | 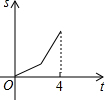 | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com