
【题目】如图,P是矩形ABCD内部的一定点,M是AB边上一动点,连接MP并延长与矩形ABCD的一边交于点N,连接AN.已知AB=6cm,设A,M两点间的距离为xcm,M,N两点间的距离为y1cm,A,N两点间的距离为y2cm.小欣根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小欣的探究过程,请补充完整;
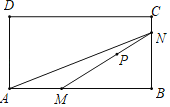
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.30 | 5.40 |
| 4.22 | 3.13 | 3.25 | 4.52 |
y2/cm | 6.30 | 6.34 | 6.43 | 6.69 | 5.75 | 4.81 | 3.98 |
(2)在同一平面直角坐标系xOy中,描出以补全后的表中各组对应值所对应的点(x,y1),并画出函数y1的图象;
(3)结合函数图象,解决问题:当△AMN为等腰三角形时,AM的长度约为 cm.
【答案】(1) 4.80 ;(2)详见解析;(3) 3.3或4.8或5.7.
【解析】
(1)根据实际取点、画图、测量,即可解决问题;
(2)利用描点法画出函数图象即可解决问题;
(3)通过图象求出直线y=x与两个函数图象的交点坐标以及函数y1与y2的交点坐标即可解决问题.
(1)根据实际取点、画图、测量,可知当AM=2cm时,y1约为4.80cm.,
故答案为4.80.
(2)两个函数图象如图所示:

(3)两个函数与直线y=x的交点为A,B,函数y1与y2的交点为C,
观察图象可知:A(3.3,3.3),B(4.8,4.8),C(5.7,4).
∴△AMN为等腰三角形时,AM的值约为3.3或4.8或5.7.
故答案为3.3或4.8或5.7.


科目:初中数学 来源: 题型:
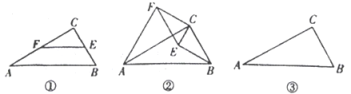
【题目】![]() 尝试探究
尝试探究
如图-![]() ,在△ABC中,∠C=90°,∠A=30°,点E、F分别是BC、AC边上的点,且EF//BC.
,在△ABC中,∠C=90°,∠A=30°,点E、F分别是BC、AC边上的点,且EF//BC.
![]()
![]() 的值为 ;
的值为 ;![]() 直线
直线![]() 与直线
与直线![]() 的位置关系为 ;
的位置关系为 ;
![]() 类比延伸
类比延伸
如图![]() ,若将图
,若将图![]() 中的
中的![]() 绕点
绕点![]() 顺时针旋转,连接
顺时针旋转,连接![]() ,则在旋转的过程中,请判断
,则在旋转的过程中,请判断![]() 的值及直线
的值及直线![]() 与直
与直![]() 线的位置关系,并说明理由;
线的位置关系,并说明理由;
![]() 拓展运用
拓展运用
若![]() ,在旋转过程中,当
,在旋转过程中,当![]() 三点在同一直线上时,请直接写出此时线段
三点在同一直线上时,请直接写出此时线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
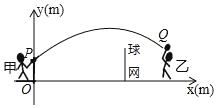
【题目】如图是甲、乙两人进行羽毛球练习赛时的一个瞬间,羽毛球飞行的高度y(m)与水平距离x(m)的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,已知点O与球网的水平距离为5m,球网的高度为1.55m.羽毛球沿水平方向运动4m时,达到羽毛球距离地面最大高度是![]() m.
m.
(1)求羽毛球经过的路线对应的函数关系式;
(2)通过计算判断此球能否过网;
(3)若甲发球过网后,羽毛球飞行到离地面的高度为![]() m的Q处时,乙扣球成功求此时乙与球网的水平距离.
m的Q处时,乙扣球成功求此时乙与球网的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
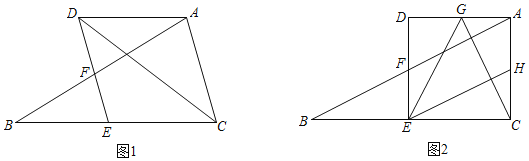
【题目】在△ABC中,过A作BC的平行线,交∠ACB的平分线于点D,点E是BC上一点,连接DE,交AB于点F,∠DEB+∠CAD=180°.
(1)如图1,求证:四边形ACED是菱形;
(2)如图2,G是AD的中点,H是AC边中点,连接CG、EG、EH,若∠ACB=90°,BC=2AC,在不添加任何辅助线的情况下,请直接写出图中与△CEH全等的三角形(不含△CEH本身).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电影公司随机收集了2000部电影的有关数据,经分类整理得到如表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
好评率 |
|
|
|
|
|
|
注:好评率是指一类电影中获得好评的部数与该类电影的部数的比值.
![]() 如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
![]() 电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化
电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化![]() 假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加
假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加![]() ,哪类电影的好评率减少
,哪类电影的好评率减少![]() ,可使改变投资策略后总的好评率达到最大?
,可使改变投资策略后总的好评率达到最大?
答:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的边长为
的边长为![]() ,顶点
,顶点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴,抛物线
轴的正半轴,抛物线![]() 经过
经过![]() 两点,点
两点,点![]() 为抛物线的顶点,连接
为抛物线的顶点,连接![]() .
.
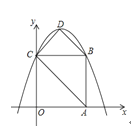
(1)求此抛物线的解析式;
(2)直接写出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过圆外一点P作⊙O的两条切线,切点分别为A、B,连接AB,在AB、PB、PA上分别取一点D、E、F,使AD=BE,BD=AF,连接DE、DF、EF,则∠EDF等于( )
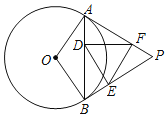
A.90°﹣∠PB.90°﹣![]() ∠PC.180°﹣∠PD.45°﹣
∠PC.180°﹣∠PD.45°﹣![]() ∠P
∠P
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com