
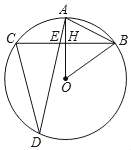
【题目】如图,⊙O的半径OA⊥弦BC于H,D是⊙O上另一点,AD与BC相交于点E,若DC=DE,OB=![]() ,AB=5.
,AB=5.
(1)求证:∠AOB=2∠ADC.
(2)求AE长.
【答案】(1)详见解析;(2)AE=![]()
【解析】
(1)根据垂径定理可得![]() ,可得∠AOC=∠AOB,根据圆周角定理可得∠AOB=2∠ADC;
,可得∠AOC=∠AOB,根据圆周角定理可得∠AOB=2∠ADC;
(2)由题意可证AB=BE=5,根据勾股定理可求AH=3,即可求EH的长,根据勾股定理可得AE的长.
证明:(1)如图,连接OC,
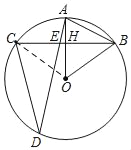
∵OA⊥BC,
∴![]() ,
,
∴∠AOC=∠AOB,
∵∠AOC=2∠ADC,
∴∠AOB=2∠ADC
(2)∵DC=DE
∴∠DCE=∠DEC
∵∠DCE=∠DAB,∠DEC=∠AEB,
∴∠AEB=∠DAB,
∴AB=BE=5
∵AH2+BH2=AB2,OH2+BH2=OB2,
∴AB2﹣AH2=BH2=OB2﹣(AO﹣AH)2,
∴![]() ,
,
∴AH=3,
∴BH=4,
∴EH=BE﹣BH=1,
∴AE=![]() =
=![]()


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
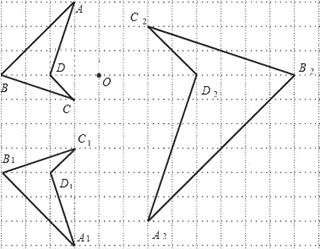
(1)图形ABCD与图形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M、N;
(2)以图中O点为位似中心,将图形ABCD放大,得到放大后的图形A2B2C2D2,则图形ABCD与图形A2B2C2D2的对应边的比是多少(注:只要写出对应边的比即可);
(3)求图形A2B2C2D2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
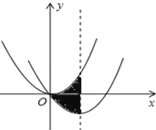
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为![]() ,则a、b的值分别为( )
,则a、b的值分别为( )
A. ![]() ,
,![]() B.
B. ![]() ,﹣
,﹣![]() C.
C. ![]() ,﹣
,﹣![]() D. ﹣
D. ﹣![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记
载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①)
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径.再次阅读后,发现AB=______寸,CD=____寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件,并帮助小智求出⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
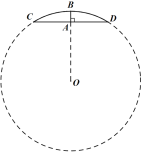
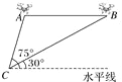
【题目】某民航飞机在大连海域失事,为调查失事原因,决定派海军潜水员打捞飞机上的黑匣子,如图所示,一潜水员在A处以每小时8海里的速度向正东方向划行,在A处测得黑匣子B在北偏东60°的方向,划行半小时后到达C处,测得黑匣子B在北偏东30°的方向,在潜水员继续向东划行多少小时,距离黑匣子B最近,并求最近距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
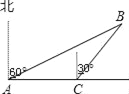
【题目】某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长( )
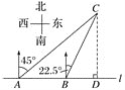
A. 2 km B. (2+![]() )km C. (4-2
)km C. (4-2![]() ) km D. (4-
) km D. (4-![]() ) km
) km
查看答案和解析>>
科目:初中数学 来源: 题型:
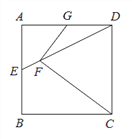
【题目】己知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE上CF=CD,过点F作FG⊥FC交AD于点G.
(1)求证:GF=GD;
(2)联结AF,求证:AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
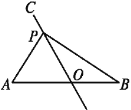
【题目】如图,某同学在一张硬纸板的中间画了一条4cm长的线段AB,过AB的中点O画直线CO,使∠AOC=60°,在直线CO上取一点P,作△PAB并剪下(纸板足够大),当剪下的△PAB为直角三角形时,AP的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com