
����Ŀ����ͼ��������y=��![]() x2+bx+c����ԭ��͵�A��6��0��������Գ��ύ�ڵ�B��P��������y=��
x2+bx+c����ԭ��͵�A��6��0��������Գ��ύ�ڵ�B��P��������y=��![]() x2+bx+c��һ���㣬����x���Ϸ�������P��x��Ĵ��߽���������y=��
x2+bx+c��һ���㣬����x���Ϸ�������P��x��Ĵ��߽���������y=��![]() ��x��h��2��hΪ�������ڵ�Q������Q��PQ�Ĵ��߽���������y=��
��x��h��2��hΪ�������ڵ�Q������Q��PQ�Ĵ��߽���������y=��![]() ��x��h��2�ڵ�Q���������Q�غϣ�������PQ�������P�ĺ�����Ϊm��
��x��h��2�ڵ�Q���������Q�غϣ�������PQ�������P�ĺ�����Ϊm��
��1����������y=��![]() x2+bx+c�ĺ�����ϵʽ����B�����ꣻ
x2+bx+c�ĺ�����ϵʽ����B�����ꣻ
��2����h=0ʱ��
����֤�� ![]() ��
��
������PQQ������OAB�ص�����ͼ�ε��ܳ�Ϊl����l��m֮��ĺ�����ϵʽ��
��3����h��0ʱ���Ƿ���ڵ�P��ʹ�ı���OAQQ��Ϊ���Σ������ڣ���ֱ��д��h��ֵ���������ڣ���˵�����ɣ�
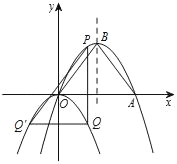
���𰸡���1��y=��![]() ��x��3��2+4����B������Ϊ��3��4������2����֤����������l=
��x��3��2+4����B������Ϊ��3��4������2����֤����������l= ��3�����ڣ�h=3��2
��3�����ڣ�h=3��2![]() ��3+2
��3+2![]() ʱ���ı���OAQQ��Ϊ����
ʱ���ı���OAQQ��Ϊ����
�������������������1���ô���ϵ������ú�������ʽ���ѽ���ʽ��Ϊ����ʽ��ֱ��д����B�����꼴�ɣ���2���ٵ�h=0ʱ����������ߵĽ���ʽ����m��ʾ����P��Q������������m��ʾ��PQ��QQ���ij������㼴�ɵý��ۣ��ڷֵ�0��m��3ʱ�͵�3��m��6ʱ���������l��m֮��ĺ�����ϵʽ����3�����ڣ����ı���OQ��1Q1A������ʱ��OQ��1=OA=Q1Q��1=6��
�������ߵĶ�����ԭ��ʱ�������Q1�������Ϊ3����x=3����y=��![]() x2���� y=-4��������ƽ�ƣ���֪Q�������겻�䣬��RT��OHQ��1���У�OH=4��OQ��1=6�����ݹ��ɶ������HQ��1=2
x2���� y=-4��������ƽ�ƣ���֪Q�������겻�䣬��RT��OHQ��1���У�OH=4��OQ��1=6�����ݹ��ɶ������HQ��1=2![]() �����ɵ�h��ֵ(���ݺ����ĶԳ���).
�����ɵ�h��ֵ(���ݺ����ĶԳ���).
���������
��1����������y=��![]() x2+bx+c����0��0���͵�A��6��0��
x2+bx+c����0��0���͵�A��6��0��
��![]() ��
��
���![]() ��
��
��������y=��![]() x2+bx+c�ĺ�����ϵʽΪ��y=��
x2+bx+c�ĺ�����ϵʽΪ��y=��![]() x2+8x��
x2+8x��
��y=��![]() ��x��3��2+4��
��x��3��2+4��
����B��������3��4����
��2����֤������h=0ʱ��������Ϊy=��![]() x2��
x2��
��P��m����![]() m2+
m2+![]() m����Q��m����
m����Q��m����![]() m2����
m2����
��PQ=![]() m��QQ��=2m��
m��QQ��=2m��
��![]() =
=![]() =
=![]() ��
��
����ͼ1�У���0��m��3ʱ����PQ��OB���ڵ�E����OA���ڵ�F��
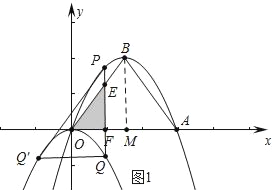
��![]() =
=![]() ����PQQ��=��BMO=90�㣬
����PQQ��=��BMO=90�㣬
���PQQ��ס�BMO��
���QPQ��=��OBM��
��EF��BM��
���OEF=��OBM��
���OEF=��QPQ�䣬
��OE��PQ�䣬
��![]() =
=![]() ��
��
��EF=![]() ��OE=
��OE=![]() ��
��
��l=OF+EF+OE=m+![]() +
+![]() m=4m��
m=4m��
��3��m��6ʱ����ͼ2�У���PQ����AB���ڵ�H����x�ύ�ڵ�G��PQ��AB��E����OA��F����HM��OA��M��

��AF=6��m��tan��EAF=![]() =
=![]() ��
��
��EF=![]() ��6��m����AE=
��6��m����AE=![]() ��
��
��tan��PGF=![]() =
=![]() ��PF=��
��PF=��![]() x2+
x2+![]() x��
x��
��GF=��![]() m2+2m��
m2+2m��
��AG=��![]() m2+m+6��
m2+m+6��
��GM=AM=��![]() m2+
m2+![]() m+3��
m+3��
��HG=HA=![]() =��
=��![]() m2+
m2+![]() m+5��
m+5��
��l=GH+EH+EF+FG=��![]() m2+4m+8��
m2+4m+8��
��������l= ��
��
��3����ͼ3�У����ڣ�
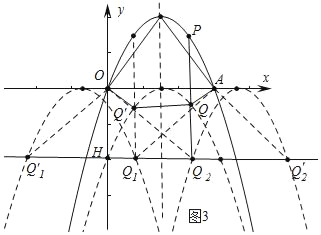
���ı���OQ��1Q1A������ʱ��OQ��1=OA=Q1Q��1=6��
��������ԭ��ʱ��Q1�������Ϊ3����x=3����
y=��![]() x2���� y=-4��������ƽ�ƣ�Q�������겻�䣬
x2���� y=-4��������ƽ�ƣ�Q�������겻�䣬
����Q1��������Ϊ-4��
��RT��OHQ��1����OH=4��OQ��1=6��
��HQ��1=2![]() ��
��
��h=3��2![]() ��3+2
��3+2![]() ��
��
��������h=3��2![]() ��3+2
��3+2![]() ʱ���ı���OAQQ��Ϊ���Σ�
ʱ���ı���OAQQ��Ϊ���Σ�


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽������������������������������������ѧ�����ˡ�վ�ˡ����˵ĺû���������һ��ѧ����һ�����ϲ������ƣ�������ͻ����һ�������أ�������ͳ�ƽ������������������������ͳ��ͼ�������ͼ��������Ϣ����������⣺

��1������α�������������ѧ��һ���ж����ˣ�
��2�����ڱ������ѧ�����������õ�ѧ����������������ͳ��ͼ����������
��3����ȫ����5��������������ô����ȫ�г������У����˺�վ�˲�����ѧ�����ж����ˣ�
���𰸡���1��500������2��75������3��2.5��
�������������������1������������������ռ�ٷֱȾ���������.(2)������������15%.
(3) ���˺�վ�˲�����ѧ����ѧ���İٷֱȳ���������.
���������
��1���⣺100��20%=500��������
����α�������������ѧ��һ����500����
��2���⣺�������õ�ѧ��������500��15%=75����
��ȫͳ��ͼ��ͼ��ʾ��

��3���⣺5������20%+30%��=2.5��
��ȫ�г������У����˺�վ�˲�����ѧ����2.5���ˣ�
�����͡������
��������
24
����Ŀ����ͼ������ABCD�У�PΪAD����һ�㣬��ֱ��BP����ABP��������EBP����A�Ķ�Ӧ��Ϊ��E����PE��CD�ཻ�ڵ�O����OE=OD��

��1����֤��PE=DH��
��2����AB=10��BC=8����DP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C��D��Բ�ϣ����ı���AOCD��ƽ���ı��Σ�����D����O�����ߣ��ֱ�OA���ӳ�����OC���ӳ����ڵ�E��F������BF.

��1����֤��BF�ǡ�O�����ߣ�
��2����֪Բ�İ뾶Ϊ1����EF�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̳�����A��B�����ͺż����������ּ������Ľ����۸�ֱ�Ϊÿ̨30Ԫ��40Ԫ���̳�����5̨A�ͺź�1̨B�ͺż��������ɻ�����76Ԫ������6̨A�ͺź�3̨B�ͺż��������ɻ�����120Ԫ�����̳�����A��B�����ͺż����������ۼ۸�ֱ��Ƕ���Ԫ��������=���ۼ۸����۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У���MΪCD�е㣬����MBC��BM��������MBE������AME �� ������ABE �� ������ �� �� �� ֮���������ϵΪ________��
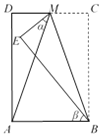
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȫ����ƽ̨�����й�����ѧ��Ϊ����ѧ����ѧ�����밲ȫ֪ʶ������ܰ�ȫ���ѵ�һ��Ӧ������.ijУΪ���˽�ҳ���ѧ������������ˮ��������������ڱ�Уѧ���������ȡ����ѧ�������飬���ռ������ݷ�Ϊ����4�����Σ�A.��ѧ���Լ����룻B.�ҳ���ѧ��һ����룻
C.���ҳ��Լ����룻 D.�ҳ���ѧ����δ����.

�����ͼ���ṩ����Ϣ������������⣺
��1������γ��������У���������________��ѧ����
��2����ȫ����ͳ��ͼ����������ͳ��ͼ�м���C������Ӧ���ε�Բ�ĽǵĶ�����
��3�����ݳ��������������Ƹ�У2000��ѧ�������ҳ���ѧ����δ������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������٣�ij��ҵ����������Ͷ�빲�����������г��������絥�����綯������2000������֪ÿ�����������ɱ�380Ԫ��ÿ̨�����絥���ɱ�1500Ԫ��2������������1�������絥��ÿ��ë��31Ԫ��4������������3�������絥��ÿ��ë��81Ԫ��
��1���������������絥��ÿ��ÿ���ֱ����ӯ������Ԫ��
��2��Ϊ����Ͷ�ʻر��ʣ�����ҵ�ƻ�Ͷ��ɱ�������174��Ԫ��ÿ�ܵ�ë��������23050Ԫ����Ҫ��Ͷ��ĵ�������Ϊ10�ı����������оٳ�����Ͷ���ʽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��EF//MN����A��B�ֱ�ΪEF��MN�ϵĶ��㣬����ACB= a��BDƽ����CBN��EF��D��
��1������FDB=120�㣬a=90�㣮��ͼ1������MBC����EAC�Ķ�����
��2���ӳ�AC��ֱ��MN��G����ʱa =80�㣬��ͼ2��GHƽ����AGB��DB�ڵ�H������GHB�Ƿ�Ϊ��ֵ�����ǣ�����ֵ�������ǣ���˵�����ɣ�


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com