
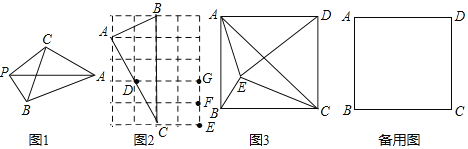
ЁОЬтФПЁПШчЭМ1ЃЌЦНУцФкгавЛЕуPЕНЁїABCЕФШ§ИіЖЅЕуЕФОрРыЗжБ№ЮЊPAЁЂPBЁЂPCЃЌШєгаPA2ЃНPB2+PC2дђГЦЕуPЮЊЁїABCЙигкЕуAЕФЙДЙЩЕуЃЎ
ЃЈ1ЃЉШчЭМ2ЃЌдк4ЁС5ЕФЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФГЄОљЮЊ1ЃЌЕуAЁЂBЁЂCЁЂDЁЂEЁЂFЁЂGОљдкаЁе§ЗНаЮЕФЖЅЕуЩЯЃЌдђЕуDЪЧЁїABCЙигкЕуЁЁ ЁЁЕФЙДЙЩЕуЃЛдкЕуEЁЂFЁЂGШ§ЕужажЛгаЕуЁЁ ЁЁЪЧЁїABCЙигкЕуAЕФЙДЙЩЕуЃЎ
ЃЈ2ЃЉШчЭМ3ЃЌEЪЧОиаЮABCDФквЛЕуЃЌЧвЕуCЪЧЁїABEЙигкЕуAЕФЙДЙЩЕуЃЌ
ЂйЧѓжЄЃКCEЃНCDЃЛ
ЂкШєDAЃНDEЃЌЁЯAECЃН120ЁуЃЌЧѓЁЯADEЕФЖШЪ§ЃЎ
ЃЈ3ЃЉОиаЮABCDжаЃЌABЃН5ЃЌBCЃН6ЃЌEЪЧОиаЮABCDФквЛЕуЃЌЧвЕуCЪЧЁїABEЙигкЕуAЕФЙДЙЩЕуЃЌШєЁїADEЪЧЕШбќШ§НЧаЮЃЌжБНгаДГіAEЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉBЃЌFЃЛЃЈ2ЃЉЂйМћНтЮіЃЌЂк40ЁуЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓAD2ЃН5ЃЌDC2ЃН5ЃЌDB2ЃН10ЃЌЕУAD2+DC2ЃНDB2ЃЌМДЕуDЪЧЁїABCЙигкЕуBЕФЙДЙЩЕуЃЛЧѓГіFA2ЃЌFB2ЃЌFC2ЃЌЕУЕНFA2+FB2ЃНFC2ЃЌМДЕуFЪЧЁїABCЙигкЕуAЕФЙДЙЩЕуЃЎ
ЃЈ2ЃЉЂйгЩОиаЮаджЪЕУЁЯADCЃН90ЁуЃЌПЩЕУAD2+DC2ЃНAC2ЃЛИљОнЙДЙЩЪ§ЕУBC2+EC2ЃНAC2ЃЌгжвђЮЊADЃНBCЃЌМДЕУCEЃНCDЃЎ
ЂкЩшЁЯCEDЃНІСЃЌИљОнЁЯAECЃН120ЁуКЭCEЃНCDМДЁЯADCЃН90ЁуЃЌПЩгУІСБэЪОЁїADEЕФШ§ИіФкНЧЃЌРћгУШ§НЧаЮФкНЧКЭ180ЁуЮЊЕШСПЙиЯЕСаЗНГЬЃЌМДЧѓГіІСНјЖјЧѓГіЁЯADEЃЎ
ЃЈ3ЃЉгЩЬѕМўЁАЕуCЪЧЁїABEЙигкЕуAЕФЙДЙЩЕуЁБШдПЩЕУCEЃНCDЃН5ЃЌзїЮЊЬѕМўЪЙгУЃЎЁїADEЪЧЕШбќШ§НЧаЮашЗж3жжЧщПіЬжТлЃЌАбУПжжЧщПіЛЭМдйИљОнОиаЮаджЪКЭЙДЙЩЖЈРэМЦЫуЃЌМДФмЧѓAEЕФГЄЃЎ
ЃЈ1ЃЉЁпDA2ЃН12+22ЃН5ЃЌDB2ЃН12+32ЃН10ЃЌDC2ЃНDA2ЃН5
ЁрDB2ЃНDC2+DA2
ЁрЕуDЪЧЁїABCЙигкЕуBЕФЙДЙЩЕу
ЁпEA2ЃН42+42ЃН32ЃЌEB2ЃН22+52ЃН29ЃЌEC2ЃН4
ЁрЕуEВЛЪЧЁїABCЕФЙДЙЩЕу
ЁпFA2ЃН32+42ЃН25ЃЌFB2ЃН22+42ЃН20ЃЌFC2ЃН12+22ЃН5
ЁрFA2ЃНFB2+FC2
ЁрЕуFЪЧЁїABCЙигкЕуAЕФЙДЙЩЕу
ЁпGA2ЃН42+22ЃН20ЃЌGB2ЃН22+32ЃН13ЃЌGC2ЃН22+22ЃН8
ЁрЕуGВЛЪЧЁїABCЕФЙДЙЩЕу
ЙЪД№АИЃКBЃЛFЃЎ
ЃЈ2ЃЉЂйжЄУїЃКШчЭМ3жаЃЌЁпЕуCЪЧЁїABEЙигкЕуAЕФЙДЙЩЕу
ЁрCA2ЃНCB2+CE2
ЁпЫФБпаЮABCDЪЧОиаЮ
ЁрABЃНCDЃЌADЃНBCЃЌЁЯADCЃН90Ёу
ЁрCA2ЃНAD2+CD2ЃНCB2+CD2
ЁрCB2+CE2ЃНCB2+CD2
ЁрCEЃНCD
ЂкШчЭМ3жаЃЌЩшЁЯCEDЃНІСЃЌдђЁЯCDEЃНЁЯCEDЃНІС
ЁрЁЯADEЃНЁЯADCЉЁЯCDEЃН90ЁуЉІС
ЁпЁЯAECЃН120Ёу
ЁрЁЯAEDЃНЁЯAECЉЁЯCEDЃН120ЁуЉІС
ЁпDAЃНDE
ЁрЁЯDAEЃНЁЯDEAЃН120ЁуЉІС
ЁпЁЯDAE+ЁЯDEA+ЁЯADEЃН180Ёу
Ёр2ЃЈ120ЁуЉІСЃЉ+ЃЈ90ЁуЉІСЃЉЃН180Ёу
НтЕУЃКІСЃН50Ёу
ЁрЁЯADEЃН90ЁуЉ50ЁуЃН40Ёу
ЃЈ3ЃЉЁпОиаЮABCDжаЃЌABЃН5ЃЌBCЃН6
ЁрADЃНBCЃН6ЃЌCDЃНABЃН5
ЁпЕуCЪЧЁїABEЙигкЕуAЕФЙДЙЩЕу
ЁрCEЃНCDЃН5
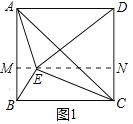
iЃЉШчЭМ1ЃЌШєDEЃНDAЃЌдђDEЃН6
Й§ЕуEзїMNЁЭABгкЕуMЃЌНЛDCгкЕуN
ЁрЁЯAMEЃНЁЯMNDЃН90Ёу
ЁрЫФБпаЮAMNDЪЧОиаЮ
ЁрMNЃНADЃН6ЃЌAMЃНDN
ЩшAMЃНDNЃНxЃЌдђCNЃНCDЉDNЃН5Љx
ЁпRtЁїDENжаЃЌEN2+DN2ЃНDE2ЃЛRtЁїCENжаЃЌEN2+CN2ЃНCE2
ЁрDE2ЉDN2ЃНCE2ЉCN2
Ёр62Љx2ЃН52ЉЃЈ5ЉxЃЉ2
НтЕУЃКxЃН![]() ЃЌ
ЃЌ
ЁрENЃН![]() ЃЌAMЃНDNЃН
ЃЌAMЃНDNЃН![]() ЃЌ
ЃЌ
ЁрMEЃНMNЉENЃН6Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрRtЁїAMEжаЃЌAEЃН![]() ЃЎ
ЃЎ
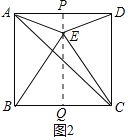
iiЃЉШчЭМ2ЃЌШєAEЃНDEЃЌдђEдкADЕФДЙжБЦНЗжЯпЩЯ
Й§ЕуEзїPQЁЭADгкЕуPЃЌНЛBCгкЕуQ
ЁрAPЃНDPЃН![]() ADЃН3ЃЌЁЯAPQЃНЁЯPQCЃН90Ёу
ADЃН3ЃЌЁЯAPQЃНЁЯPQCЃН90Ёу
ЁрЫФБпаЮCDPQЪЧОиаЮ
ЁрPQЃНCDЃН5ЃЌCQЃНPDЃН3
ЁрRtЁїCQEжаЃЌEQЃН![]()
ЁрPEЃНPQЉEQЃН1
ЁрRtЁїAPEжаЃЌAEЃН![]()
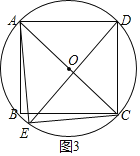
iiiЃЉШчЭМ3ЃЌШєAEЃНADЃН6ЃЌдђAE2+CE2ЃНAD2+CD2ЃНAC2
ЁрЁЯAECЃН90Ёу
ШЁACжаЕуOЃЌдђЕуAЁЂBЁЂCЁЂDдквдOЮЊдВаФЁЂOAЮЊАыОЖЕФЁбOЩЯ
ЁрЕуEвВдкЁбOЩЯ
ЁрЕуEВЛдкОиаЮABCDФкВПЃЌВЛЗћКЯЬтвт
злЩЯЫљЪіЃЌШєЁїADEЪЧЕШбќШ§НЧаЮЃЌAEЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 ЛЦИдаЁзДдЊПкЫуЫйЫуСЗЯАВсЯЕСаД№АИ
ЛЦИдаЁзДдЊПкЫуЫйЫуСЗЯАВсЯЕСаД№АИ ГЩЙІбЕСЗМЦЛЎЯЕСаД№АИ
ГЩЙІбЕСЗМЦЛЎЯЕСаД№АИ БЖЫйбЕСЗЗЈжБЭЈжаПМПМЕуЯЕСаД№АИ
БЖЫйбЕСЗЗЈжБЭЈжаПМПМЕуЯЕСаД№АИ вЛОэИуЖЈЯЕСаД№АИ
вЛОэИуЖЈЯЕСаД№АИ УћаЃзївЕБОЯЕСаД№АИ
УћаЃзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬвЛЈжабЇМЦЛЎЙКТђ![]() СНжжаЭКХЕФаЁКкАхЃЌОЧЂЬИЃЌ ЙКТђвЛПщ
СНжжаЭКХЕФаЁКкАхЃЌОЧЂЬИЃЌ ЙКТђвЛПщ![]() аЭаЁКкАхБШТђвЛПщ
аЭаЁКкАхБШТђвЛПщ![]() аЭаЁКкАхЖр
аЭаЁКкАхЖр![]() дЊЃЌЧвЙКТђ
дЊЃЌЧвЙКТђ![]() Пщ
Пщ![]() аЭаЁКкАхКЭ
аЭаЁКкАхКЭ![]() Пщ
Пщ![]() аЭаЁКкАхЙВаш
аЭаЁКкАхЙВаш![]() дЊЃЎ
дЊЃЎ
ЃЈ1ЃЉЧѓЙКТђвЛПщ![]() аЭаЁКкАхКЭвЛПщ
аЭаЁКкАхКЭвЛПщ![]() аЭаЁКкАхИїашвЊЖрЩйдЊЃП
аЭаЁКкАхИїашвЊЖрЩйдЊЃП
ЃЈ2ЃЉИљОнбЇаЃЕФЪЕМЪЧщПіЃЌашЙКТђ![]() СНжжаЭКХЕФаЁКкАхЙВ
СНжжаЭКХЕФаЁКкАхЙВ![]() ПщЃЌВЂЧвЙКТђ
ПщЃЌВЂЧвЙКТђ![]() аЭаЁКкАхЕФЪ§СПВЛЩйгкЙКТђ
аЭаЁКкАхЕФЪ§СПВЛЩйгкЙКТђ![]() аЭаЁКкАхЕФЪ§СПЃЌЧыЮЪбЇаЃЙКТђетХњаЁКкАхзюЩйвЊЖрЩйдЊЃП
аЭаЁКкАхЕФЪ§СПЃЌЧыЮЪбЇаЃЙКТђетХњаЁКкАхзюЩйвЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2-4ax+c(aЁй0)гыyжсНЛгкЕуAЃЌНЋЕуAЯђгвЦНвЦ2ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуB.жБЯп![]() гыxжсЃЌyжсЗжБ№НЛгкЕуCЃЌD.
гыxжсЃЌyжсЗжБ№НЛгкЕуCЃЌD.
ЃЈ1ЃЉЧѓХзЮяЯпЕФЖдГЦжс.
ЃЈ2ЃЉШєЕуAгыЕуDЙигкxжсЖдГЦ.
ЂйЧѓЕуBЕФзјБъ.
ЂкШєХзЮяЯпгыЯпЖЮBCЧЁгавЛИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓaЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАыдВOЕФжБОЖABЃН5cmЃЌЕуMдкABЩЯЧвAMЃН1cmЃЌЕуPЪЧАыдВOЩЯЕФЖЏЕуЃЌЙ§ЕуBзїBQЁЭPMНЛPMЃЈЛђPMЕФбгГЄЯпЃЉгкЕуQЃЎЩшPMЃНxcmЃЌBQЃНycmЃЎЃЈЕБЕуPгыЕуAЛђЕуBжиКЯЪБЃЌyЕФжЕЮЊ0ЃЉаЁЪЏИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§yЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎЯТУцЪЧаЁЪЏЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
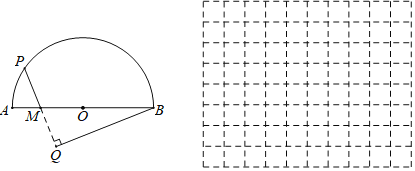
ЃЈ1ЃЉЭЈЙ§ШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНСЫxгыyЕФМИзщжЕЃЌШчЯТБэЃК
x/cm | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 0 | 3.7 | ______ | 3.8 | 3.3 | 2.5 | ______ |
ЃЈ2ЃЉНЈСЂЦНУцжБНЧзјБъЯЕЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБBQгыжБОЖABЫљМаЕФШёНЧЮЊ60ЁуЪБЃЌPMЕФГЄЖШдМЮЊ______cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABCDЃЌЕуEЪЧBCБпЩЯЕФвЛЕуЃЌНЋБпADбгГЄжСЕуFЃЌЪЙЁЯAFCЃНЁЯDEC.
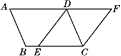
(1)ЧѓжЄЃКЫФБпаЮDECFЪЧЦНааЫФБпаЮЃЛ
(2)ШєABЃН13ЃЌDFЃН14ЃЌtan AЃН![]() ЃЌЧѓCFЕФГЄЃЎ
ЃЌЧѓCFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПAЁЂBСНЫљбЇаЃЕФбЇЩњЖМВЮМгСЫФГДЮЬхг§ВтЪдЃЌГЩМЈОљЮЊ7Љ10ЗжЃЌЧвЮЊећЪ§ЃЎССССЗжБ№ДгетСНЫљбЇаЃИїЫцЛњГщШЁвЛВПЗжбЇЩњЕФВтЪдГЩМЈЃЌЙВ200ЗнЃЌВЂЛцжЦСЫШчЯТЩаВЛЭъећЕФЭГМЦЭМЃЎ
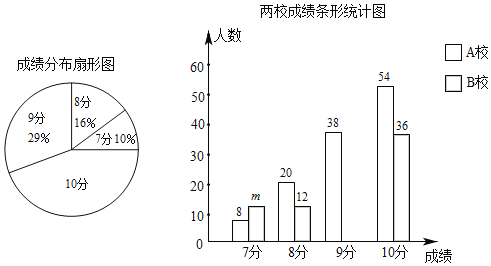
ЃЈ1ЃЉет200ЗнВтЪдГЩМЈЕФжаЮЛЪ§ЪЧЁЁ ЁЁЗжЃЌmЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛЩШаЮЭГМЦЭМжаЃЌЧѓГЩМЈЮЊ10ЗжЫљдкЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЎ
ЃЈ3ЃЉССССЫуГіСЫЁА1УћAаЃбЇЩњЕФГЩМЈБЛГщЕНЁБЕФИХТЪЪЧ![]() ЃЌЧыФуЙРМЦAаЃГЩМЈЮЊ8ЗжЕФбЇЩњДѓдМгаЖрЩйУћЃЎ
ЃЌЧыФуЙРМЦAаЃГЩМЈЮЊ8ЗжЕФбЇЩњДѓдМгаЖрЩйУћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИлжщАФДѓЧХЪЧжаЙњОГФквЛзљСЌНгЯуИлЁЂжщКЃКЭАФУХЕФЧХЫэЙЄГЬЃЌЮЛгкжаЙњЙуЖЋЪЁСциъбѓЧјгђФкЃЌЮЊжщНШ§НЧжоЕиЧјЛЗЯпИпЫйЙЋТЗФЯЛЗЖЮЃЌЧржнКНЕРЧХЁАжаЙњНсШ§ЕиЭЌаФЁБжїЬтЕФаБРЫїЫўШчЭМЃЈ1ЃЉЫљЪО.ФГЪ§бЇаЫШЄаЁзщИљОнВФСЯБржЦСЫШчЯТЪ§бЇЮЪЬтЃЌЧыФуНтД№.
ШчЭМЃЈ2ЃЉЃЌBCЃЌDEЮЊжїЫўABЃЈжїЫўABгыЧХУцACДЙжБЃЉЩЯЕФСНЬѕИжЫїЃЌЧХУцЩЯCЁЂDСНЕуМфЕФОрРыЮЊ16mЃЌжїЫўЩЯAЁЂEСНЕуЕФОрРыЮЊ18.4mЃЌвбжЊBCгыЧХУцACЕФМаНЧЮЊ30ЁуЃЌDEгыЧХУцACЕФМаНЧЮЊ38ЁуЁЃЧѓжїЫўABЕФИп.ЃЈНсЙћОЋШЗЕН1УзЃЌВЮПМЪ§ОнЃКsin38ЁуЁж0.6ЃЌcos38ЁуЁж0.8ЃЌtan38ЁуЁж0.8ЃЌ![]() Ёж1.7ЃЉ
Ёж1.7ЃЉ

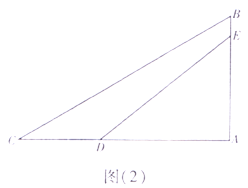
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАЫФъМЖЃЈ1ЃЉАрбаОПадбЇЯАаЁзщЮЊбаОПШЋаЃЭЌбЇПЮЭтдФЖСЧщПіЃЌдкШЋаЃЫцЛњбћЧыСЫВПЗжЭЌбЇВЮгыЮЪОэЕїВщЃЌЭГМЦЭЌбЇУЧвЛИідТдФЖСПЮЭтЪщЕФЪ§СПЃЌВЂЛцжЦСЫвдЯТЭГМЦЭМЃЎ
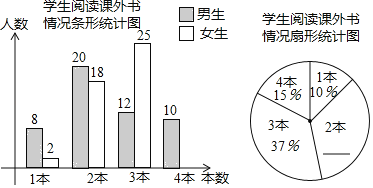
ЧыИљОнЭМжааХЯЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЙВгаЖрЩйУћЭЌбЇВЮгыЮЪОэЕїВщЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШЋаЃЙВгабЇЩњ1500ШЫЃЌЧыЙРМЦИУаЃбЇЩњвЛИідТдФЖС2БОПЮЭтЪщЕФШЫЪ§дМЮЊЖрЩйЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() вЛЖЏЕуЃЌШєНЋ
вЛЖЏЕуЃЌШєНЋ![]() би
би![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() ТфдкЦНУцЩЯЕФЕу
ТфдкЦНУцЩЯЕФЕу![]() ДІЃЌСЌНс
ДІЃЌСЌНс![]() ЃЎШє
ЃЎШє![]() Ш§ЕудквЛжБЯпЩЯЃЌдђ
Ш§ЕудквЛжБЯпЩЯЃЌдђ![]() ____ЃЎ
____ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com