
����Ŀ��A��B����ѧУ��ѧ�����μ���ij���������ԣ��ɼ���Ϊ7��10�֣���Ϊ�����������ֱ��������ѧУ�������ȡһ����ѧ���IJ��Գɼ�����200�ݣ��������������в�������ͳ��ͼ��
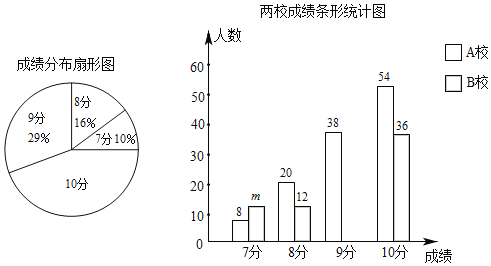
��1����200�ݲ��Գɼ�����λ������ ���֣�m���� ����
��2����ȫ����ͳ��ͼ������ͳ��ͼ�У���ɼ�Ϊ10���������ε�Բ�ĽǵĶ�����
��3����������ˡ�1��AУѧ���ijɼ����鵽���ĸ�����![]() ���������AУ�ɼ�Ϊ8�ֵ�ѧ����Լ�ж�������
���������AУ�ɼ�Ϊ8�ֵ�ѧ����Լ�ж�������
���𰸡���1��9��12��,��2����ͼ��������162�㣻��3��220��
��������
��1��������λ���Ķ��弴�ɵõ��𰸣�
��2����������ͳ��ͼ�е����ݲ�ȫ����ͳ��ͼ�������õ��ɼ�Ϊ10���������ε�Բ�ĽǵĶ��������ɣ�
��3�������AУ��������8+20+38+54����![]() ��1320���������ټ���AУ�ɼ�Ϊ8�ֵ�ѧ����,���ɣ�
��1320���������ټ���AУ�ɼ�Ϊ8�ֵ�ѧ����,���ɣ�
��1��������ã�����Щ�ɼ�����С���к�100��101 λ������9�֣�����λ����9��
m����20+12����16%��10%��8��12��������
�ʴ�Ϊ��9��12��
��2��BУ�ɼ�Ϊ9�ֵ�����Ϊ��200��29%��38��20��������
��ȫ����ͳ��ͼ��ͼ��ʾ��

�ɼ�Ϊ10���������ε�Բ�ĽǵĶ���Ϊ![]() ��360�㣽162�㣻
��360�㣽162�㣻
��3��������ɵ�����8+20+38+54����![]() ��1320��������
��1320��������
1320��![]() ��220��������
��220��������
��AУ�ɼ�Ϊ8�ֵ�ѧ����Լ��220����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
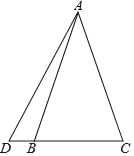
����Ŀ����֪��ͼ����ABCΪ���������Σ�DΪCB�ӳ�����һ�㣬��AD�ҡ�DAC��45�㣬BD��1��CB��4����AC��Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2��x��c�ĶԳ���Ϊֱ��x����1����x�ύ�ڵ�A����4��0���͵�B����y�ύ�ڵ�C����D��m��n��Ϊ��������һ�㣬��OΪ����ԭ�㣮
��1���������ߵĽ���ʽ��
��2����m��0����DAB����BCO������AD�������߽��ڵ�H���뻭��ͼ�Σ������H�����ꣻ
��3����n��5��m����1��ֱ��DE��DF������x�ᴹֱ������������ֻ��һ�������㣬DE��DF�ֱ���Գ��ύ�ڵ�M��N����PΪ�Գ����ϣ�M��N�·���һ�㣬��PD2��PMPNʱ���뻭��ͼ�Σ������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
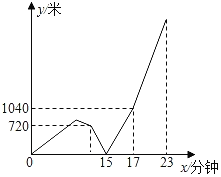
����Ŀ��С�մӼҳ������ٲ���ȥѧУ��ѧ�������Ӻ���������ѧ��ҵ�����ǵ�ͷԭ�ٷ��ز�������绰���ְ֣��Ҷϵ绰��ְ����������ܲ�ȥС�գ�ͬʱС����ԭ�ٵ����������ܲ��ؼң��ְ���С�պ���ԭ�ٵ�![]() ��ԭ·���лؼң�����ʱ���ϵС���õ���ҵ��ͬ����֮ǰ�ܲ����ٶȸ���ѧУ�����ڴӼҳ�����23���ӵ�У��С�ձ��ְ���ʱ����ʱ����Բ��ƣ�������֮������·��y���ף���С�մӼҳ�����ѧУ�IJ���ʱ��x�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ����С�ռҵ�ѧУ��·��Ϊ_____�ף�
��ԭ·���лؼң�����ʱ���ϵС���õ���ҵ��ͬ����֮ǰ�ܲ����ٶȸ���ѧУ�����ڴӼҳ�����23���ӵ�У��С�ձ��ְ���ʱ����ʱ����Բ��ƣ�������֮������·��y���ף���С�մӼҳ�����ѧУ�IJ���ʱ��x�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ����С�ռҵ�ѧУ��·��Ϊ_____�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ѿ�֪��һЩ����Ĺ����������������������еĹ�������3��4��5������������ż���еĹ�����6��8��10����ʵ�ϣ�������������������Ȼ�ǹ�������
(1)��������һЩ���ɹ������Ĺ�ʽҲ����д������������ϴ����˹ѧ������Ĺ�ʽ��a��2n+1��b��2n2+2n��c��2n2+2n+1(nΪ������)��һ�鹴��������֤���������Ϲ�ʽ��a��b��c������һ�鹴������
(2)Ȼ���������ϵ�һ�θ����Ĺ�������ʽ���ռ����ҹ��Ŵ���������ѧ�����������������У������ᵽ����a��![]() (m2��n2)��b��mn��c��
(m2��n2)��b��mn��c��![]() (m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
(m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
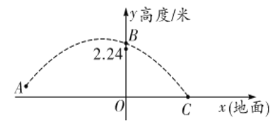
����Ŀ��2019��Ů�����籭��9�����ձ����У��й�Ů����ʮһ��ʤ�Ľ��˳ɼ�����ھ������չ�����Ŷ�Э������ǿƴ����Ů�ž�����ͼ��ij�α����е���ʱ�Ķ��������������������˶�·�߽��ƵĿ��������ߣ���ͬһ��ֱƽ���ڽ�����ͼ��ʾ��ֱ������ϵ����֪�˶�Ա����ʱ��ͼ�е�![]() ����������ˮƽ����Ϊ5�ף����������Ĵ�ֱ����Ϊ0.5�ף������������϶�0.26�״���ͼ�е�
����������ˮƽ����Ϊ5�ף����������Ĵ�ֱ����Ϊ0.5�ף������������϶�0.26�״���ͼ�е�![]() ��Խ��������Ů���������������϶˾����ĸ߶�Ϊ2.24�ף������ʱ��ͼ�е�
��Խ��������Ů���������������϶˾����ĸ߶�Ϊ2.24�ף������ʱ��ͼ�е�![]() ����������ˮƽ����Ϊ2.5�ף��������˶�·�ߵĺ�������ʽΪ�� ��
����������ˮƽ����Ϊ2.5�ף��������˶�·�ߵĺ�������ʽΪ�� ��

A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�����龳
��ѧ����ϣ���ʦ��ͬѧ���ԡ������ε���ת��Ϊ���չ��ѧ���![]() ��
��![]() ������ȫ�ȵ�ֱ��������ֽƬ������
������ȫ�ȵ�ֱ��������ֽƬ������![]() ��
��![]() ��
��![]() ��
��
�������
��1����ͼ�٣��ǻ�С�齫![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת�����ֵ���
˳ʱ����ת�����ֵ���![]() ǡ������
ǡ������![]() ����ʱ��
����ʱ��![]() �����������֤��������ۣ�
�����������֤��������ۣ�
��2������С�����ǻ�С��Ļ����ϼ���̽��������![]() ����
����![]() C�Ƶ�
C�Ƶ�![]() ������ת����ͼ����ʾ��λ��ʱ���������
������ת����ͼ����ʾ��λ��ʱ���������![]() �������������֤��һ�����Ƿ���ȷ����˵�����ɣ�
�������������֤��һ�����Ƿ���ȷ����˵�����ɣ�
̽������
��3����ͼ�ۣ��ڷ�С����ǰ����С��������£�������ת![]() ����
����![]() ���㹲��ʱ����
���㹲��ʱ����![]() �ij���
�ij���
��4����ͼ�ٵĻ����ϣ�д��һ���߳���Ϊ![]() �������Σ���������ĸ����
�������Σ���������ĸ����
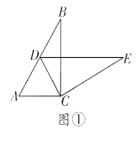
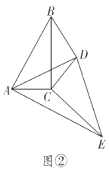
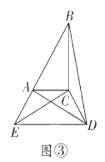
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�����꼶ѧ����˯������������ȡ�˸������꼶ѧ������ѧ�����е���.��֪D���ѧ����15�ˣ����ó������õ����ݻ�����ʾ��ͳ��ͼ��.
һ��ѧ��˯��������������λ��Сʱ��
��� | ˯��ʱ�� |
|
|
|
|
|
|
|
|
|
|
����ѧ��˯�����ͳ��ͼ

����ͼ���ṩ����Ϣ���ش��������⣺
��1�����������꼶ѧ��˯�����ͳ��ͼ���е�a��ֵ��a��Ӧ�����ε�Բ�ĽǶ�����
��2�����˯��ʱ��x��ʱ�����㣺![]() ����˯��ʱ��ϸ�.��֪�������꼶ѧ����3250�ˣ��Թ��Ƹ������꼶ѧ��˯��ʱ��ϸ�Ĺ��ж����ˣ�
����˯��ʱ��ϸ�.��֪�������꼶ѧ����3250�ˣ��Թ��Ƹ������꼶ѧ��˯��ʱ��ϸ�Ĺ��ж����ˣ�
��3������������ѧ��˯������������Сֵ����C����У�ȡ![]() ����B��C��D����ѧ����ƽ��˯��ʱ����Ϊ���꼶ѧ����˯��ʱ�������.����������꼶ѧ����ƽ��˯��ʱ��.
����B��C��D����ѧ����ƽ��˯��ʱ����Ϊ���꼶ѧ����˯��ʱ�������.����������꼶ѧ����ƽ��˯��ʱ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��![]() x2+
x2+![]() x��1��x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C���䶥��ΪD����������λ��ֱ��l��y=t��t��
x��1��x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C���䶥��ΪD����������λ��ֱ��l��y=t��t��![]() ���Ϸ��IJ�����ֱ��l���·��ۣ�������ʣ�ಿ���뷭�ۺ�����ͼ�����һ����M���ε���ͼ��
���Ϸ��IJ�����ֱ��l���·��ۣ�������ʣ�ಿ���뷭�ۺ�����ͼ�����һ����M���ε���ͼ��
��1�����A��B��D������
��2����ͼ�٣������߷��ۺ�D���ڵ�E��������E����ABC�ڣ����߽磩ʱ����t��ȡֵ��Χ��
��3����ͼ�ڣ���t=0ʱ����Q����M������ͼ����һ���㣬�Ƿ������CQΪֱ����Բ��x�������ڵ�P�������ڣ�ֱ��д������P�����꣮
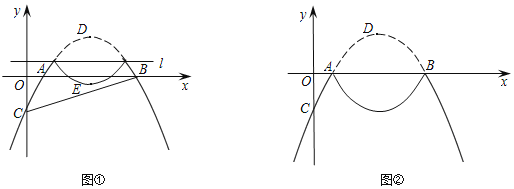
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com