
【题目】抛物线y=﹣![]() x2+
x2+![]() x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<
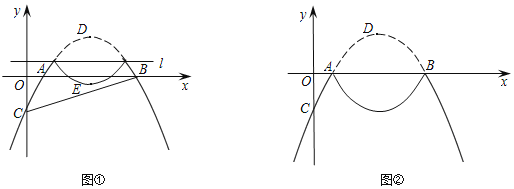
x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<![]() )上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
)上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
(1)求点A,B,D的坐标
(2)如图①,抛物线翻折后,点D落在点E处.当点E在△ABC内(含边界)时,求t的取值范围;
(3)如图②,当t=0时,若Q是“M”形新图象上一动点,是否存在以CQ为直径的圆与x轴相切于点P?若存在,直接写出出点P的坐标.
【答案】(1)点A的坐标为(![]() ,0),点B的坐标为(3,0),点D的坐标为(
,0),点B的坐标为(3,0),点D的坐标为(![]() ,
,![]() );(2)
);(2)![]() ≤t≤
≤t≤![]() ;(3)存在,点P的坐标为(
;(3)存在,点P的坐标为(![]() ,0)、(
,0)、(![]() ,0)或(
,0)或(![]() ,0)、(1,0).
,0)、(1,0).
【解析】
(1)利用二次函数图象上点的坐标特征可求出点A、B的坐标,再利用配方法即可找出抛物线的顶点D的坐标;
(2)由点D的坐标结合对称找出点E的坐标,根据点B、C的坐标利用待定系数法可求出直线BC的解析式,再利用一次函数图象上点的坐标特征即可得出关于t的一元一次不等式组,解之即可得出t的取值范围;
(3)假设存在,设点P的坐标为(![]() m,0),则点Q的横坐标为m,分m<
m,0),则点Q的横坐标为m,分m<![]() 或m>3及
或m>3及![]() ≤m≤3两种情况,利用勾股定理找出关于m的一元二次方程,解之即可得出m的值,进而可找出点P的坐标,此题得解.
≤m≤3两种情况,利用勾股定理找出关于m的一元二次方程,解之即可得出m的值,进而可找出点P的坐标,此题得解.
解:(1)当y=0时,有﹣![]() x2+
x2+![]() x﹣1=0,
x﹣1=0,
解得:x1=![]() ,x2=3,
,x2=3,
∴点A的坐标为(![]() ,0),点B的坐标为(3,0).
,0),点B的坐标为(3,0).
∵y=﹣![]() x2+
x2+![]() x﹣1=﹣
x﹣1=﹣![]() (x2﹣
(x2﹣![]() x)﹣1=﹣
x)﹣1=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴点D的坐标为(![]() ,
,![]() ).
).
(2)∵点E、点D关于直线y=t对称,
∴点E的坐标为(![]() ,2t﹣
,2t﹣![]() ).
).
当x=0时,y=﹣![]() x2+
x2+![]() x﹣1=﹣1,
x﹣1=﹣1,
∴点C的坐标为(0,﹣1).
设线段BC所在直线的解析式为y=kx+b,
将B(3,0)、C(0,﹣1)代入y=kx+b,
![]() 解得:
解得: ![]() ,
,
∴线段BC所在直线的解析式为y=![]() x﹣1.
x﹣1.
∵点E在△ABC内(含边界),
∴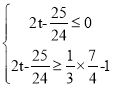 ,
,
解得:![]() ≤t≤
≤t≤![]() .
.
(3)当x<![]() 或x>3时,y=-
或x>3时,y=-![]() x2+
x2+![]() x-1;
x-1;
当![]() ≤x≤3时,y=
≤x≤3时,y=![]() x2-
x2-![]() x+1.
x+1.
假设存在,设点P的坐标为(![]() m,0),则点Q的横坐标为m.
m,0),则点Q的横坐标为m.
①当m<![]() 或m>3时,点Q的坐标为(m,-
或m>3时,点Q的坐标为(m,-![]() m2+
m2+![]() m-1)(如图1),
m-1)(如图1),
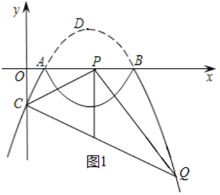
∵以CQ为直径的圆与x轴相切于点P,
∴CP⊥PQ,
∴CQ2=CP2+PQ2,即m2+(-![]() m2+
m2+![]() m)2=
m)2=![]() m2+1+
m2+1+![]() m2+(-
m2+(-![]() m2+
m2+![]() m-1)2,
m-1)2,
整理,得:m1=![]() ,m2=
,m2=![]() ,
,
∴点P的坐标为(![]() ,0)或(
,0)或(![]() ,0);
,0);
②当![]() ≤m≤3时,点Q的坐标为(m,
≤m≤3时,点Q的坐标为(m,![]() m2-
m2-![]() m+1)(如图2),
m+1)(如图2),
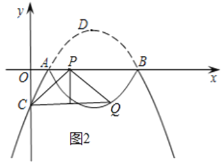
∵以CQ为直径的圆与x轴相切于点P,
∴CP⊥PQ,
∴CQ2=CP2+PQ2,即m2+(![]() m2-
m2-![]() m+2)2=
m+2)2=![]() m2+1+
m2+1+![]() m2+(
m2+(![]() m2-
m2-![]() m+1)2,
m+1)2,
整理,得:11m2-28m+12=0,
解得:m3=![]() ,m4=2,
,m4=2,
∴点P的坐标为(![]() ,0)或(1,0).
,0)或(1,0).
综上所述:存在以CQ为直径的圆与x轴相切于点P,点P的坐标为(![]() ,0)、(
,0)、(![]() ,0)、(1,0)或(
,0)、(1,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】A、B两所学校的学生都参加了某次体育测试,成绩均为7﹣10分,且为整数.亮亮分别从这两所学校各随机抽取一部分学生的测试成绩,共200份,并绘制了如下尚不完整的统计图.
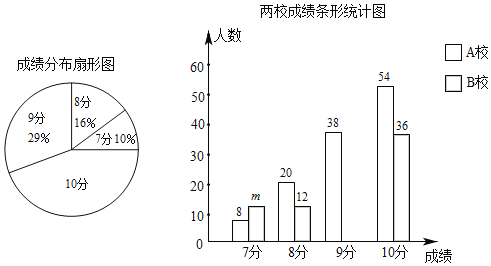
(1)这200份测试成绩的中位数是 分,m= ;
(2)补全条形统计图;扇形统计图中,求成绩为10分所在扇形的圆心角的度数.
(3)亮亮算出了“1名A校学生的成绩被抽到”的概率是![]() ,请你估计A校成绩为8分的学生大约有多少名.
,请你估计A校成绩为8分的学生大约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
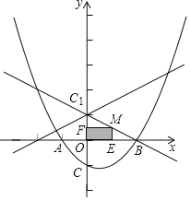
【题目】如图,已知抛物线y=ax2+bx﹣1与x轴的交点为A(﹣1,0),B(2,0),且与y轴交于C点.
(1)求该抛物线的表达式;
(2)点C关于x轴的对称点为C1,M是线段BC1上的一个动点(不与B、C1重合),ME⊥x轴,MF⊥y轴,垂足分别为E、F,当点M在什么位置时,矩形MFOE的面积最大?说明理由.
(3)已知点P是直线y=![]() x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场家电专柜购进一批甲,乙两种电器,甲种电器共用了10 350元,乙种电器共用了9 600元,甲种电器的件数是乙种电器的1.5倍,甲种电器每件的进价比乙种电器每件的进价少90元.
(1)甲、乙两种电器各购进多少件?
(2)商场购进两种电器后,按进价提高40%后标价销售,很快全部售完,求售完这批电器商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
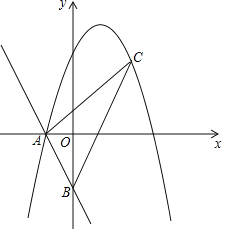
【题目】一次函数y=﹣2x﹣2分别与x轴、y轴交于点A、B.顶点为(1,4)的抛物线经过点A.
(1)求抛物线的解析式;
(2)点C为第一象限抛物线上一动点.设点C的横坐标为m,△ABC的面积为S.当m为何值时,S的值最大,并求S的最大值;
(3)在(2)的结论下,若点M在y轴上,△ACM为直角三角形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
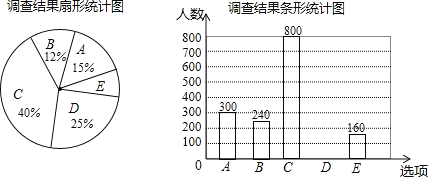
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .若已知
.若已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() .(若同学们打印的BC的长度如不是
.(若同学们打印的BC的长度如不是![]() ,请同学们重新画图、测量)
,请同学们重新画图、测量)
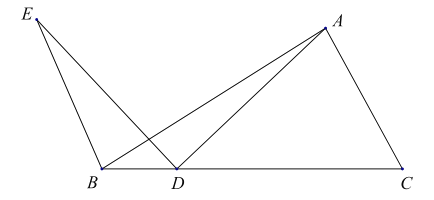
小明根据学习函数的经验,分别对![]() 自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
|
| 5.66 | 4.32 |
| 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
写出![]() 的值.(保留1位小数)
的值.(保留1位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
(3)结合函数图像,解决问题:
①当![]() 在线段
在线段![]() 上时,
上时,![]() 的长度约为________
的长度约为________![]() ;
;
②当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度
的长度![]() 约为_______
约为_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
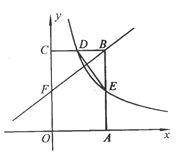
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,4),双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形 ![]() 中,点
中,点![]() 是射线
是射线 ![]() 上一个动点.连接
上一个动点.连接![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() .
.
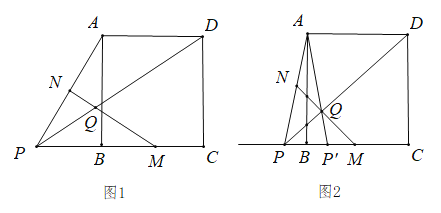
(1)如图 1,当点![]() 在线段
在线段 ![]() 的延长线上时,请判断
的延长线上时,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
(2)如图 2,正方形 的边长为 4,点![]() 与点
与点![]() 关于直线
关于直线 ![]() 对称,且点
对称,且点![]() 在线段
在线段 ![]() 上.连接
上.连接![]() ,若点
,若点 ![]() 恰好在直线
恰好在直线![]() 上,求
上,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com