
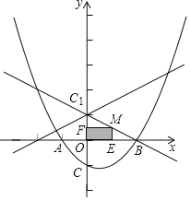
【题目】如图,已知抛物线y=ax2+bx﹣1与x轴的交点为A(﹣1,0),B(2,0),且与y轴交于C点.
(1)求该抛物线的表达式;
(2)点C关于x轴的对称点为C1,M是线段BC1上的一个动点(不与B、C1重合),ME⊥x轴,MF⊥y轴,垂足分别为E、F,当点M在什么位置时,矩形MFOE的面积最大?说明理由.
(3)已知点P是直线y=![]() x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
【答案】(1) ![]() ;(2)点M为线段C1B中点时,S矩形MFOE最大,理由见解析;(3) 点P和点Q的坐标为P1(4,3),Q1(4,5)或P2(﹣2,0),Q2(﹣2,2)或P3(2,2),Q3(2,0)或P4(﹣2,0),Q4(2,0).
;(2)点M为线段C1B中点时,S矩形MFOE最大,理由见解析;(3) 点P和点Q的坐标为P1(4,3),Q1(4,5)或P2(﹣2,0),Q2(﹣2,2)或P3(2,2),Q3(2,0)或P4(﹣2,0),Q4(2,0).
【解析】
(1)将A(﹣1,0),B(2,0)分别代入解析式即可解答
(2)令x=0,y=﹣1,得出C的坐标,再利用对称轴的性质得出C1,将B(2,0),C1(0,1)分别代入直线C1B解析式,得出直线C1B的解析式,设M(t,![]() ),则 E(t,0),F(0,
),则 E(t,0),F(0,![]() ),根据矩形的面积公式即可解答
),根据矩形的面积公式即可解答
(3)根据题意可分情况讨论①当C1C为边,则C1C∥PQ,C1C=PQ,设P(m,![]() m+1),Q(m,
m+1),Q(m,![]() ),求出m即可解答;②C1C为对角线,∵C1C与PQ互相平分,C1C的中点为(0,0),PQ的中点为(0,0),设P(m,
),求出m即可解答;②C1C为对角线,∵C1C与PQ互相平分,C1C的中点为(0,0),PQ的中点为(0,0),设P(m,![]() m+1),则Q(﹣m,
m+1),则Q(﹣m,![]() ),求出m即可
),求出m即可
(1)将A(﹣1,0),B(2,0)分别代入抛物线y=ax2+bx﹣1中,得![]() ,解得:
,解得: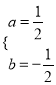
∴该抛物线的表达式为:![]() .
.
(2)在![]() 中,令x=0,y=﹣1,∴C(0,﹣1)
中,令x=0,y=﹣1,∴C(0,﹣1)
∵点C关于x轴的对称点为C1,
∴C1(0,1),设直线C1B解析式为y=kx+b,将B(2,0),C1(0,1)分别代入得![]() ,解得
,解得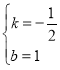 ,
,
∴直线C1B解析式为![]() ,设M(t,
,设M(t,![]() ),则 E(t,0),F(0,
),则 E(t,0),F(0,![]() )
)
∴S矩形MFOE=OE×OF=t(![]() )=﹣
)=﹣![]() (t﹣1)2+
(t﹣1)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当t=1时,S矩形MFOE最大值=![]() ,此时,M(1,
,此时,M(1,![]() );即点M为线段C1B中点时,S矩形MFOE最大.
);即点M为线段C1B中点时,S矩形MFOE最大.
(3)由题意,C(0,﹣1),C1(0,1),以C、C1、P、Q为顶点的四边形为平行四边形,分以下两种情况:
①C1C为边,则C1C∥PQ,C1C=PQ,设P(m,![]() m+1),Q(m,
m+1),Q(m,![]() ),
),
∴|(![]() )﹣(
)﹣(![]() m+1)|=2,解得:m1=4,m2=﹣2,m3=2,m4=0(舍),
m+1)|=2,解得:m1=4,m2=﹣2,m3=2,m4=0(舍),
P1(4,3),Q1(4,5);P2(﹣2,0),Q2(﹣2,2);P3(2,2),Q3(2,0)
②C1C为对角线,∵C1C与PQ互相平分,C1C的中点为(0,0),
∴PQ的中点为(0,0),设P(m,![]() m+1),则Q(﹣m,
m+1),则Q(﹣m,![]() )
)
∴(![]() m+1)+(
m+1)+(![]() )=0,解得:m1=0(舍去),m2=﹣2,
)=0,解得:m1=0(舍去),m2=﹣2,
∴P4(﹣2,0),Q4(2,0);
综上所述,点P和点Q的坐标为:P1(4,3),Q1(4,5)或P2(﹣2,0),Q2(﹣2,2)或P3(2,2),Q3(2,0)或P4(﹣2,0),Q4(2,0).


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-x+c的对称轴为直线x=-1,与x轴交于点A(-4,0)和点B,与y轴交于点C,点D(m,n)为坐标轴中一点,点O为坐标原点.
(1)求抛物线的解析式;
(2)若m=0,∠DAB=∠BCO,射线AD与抛物线交于点H,请画出图形,求出点H的坐标;
(3)若n=5,m≠-1,直线DE和DF(不与x轴垂直)都与抛物线只有一个公共点,DE和DF分别与对称轴交于点M,N,点P为对称轴上(M,N下方)一点,当PD2=PMPN时,请画出图形,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,![]() 和
和![]() 是两个全等的直角三角形纸片,其中
是两个全等的直角三角形纸片,其中![]() ,
,![]() ,
,![]() .
.
解决问题
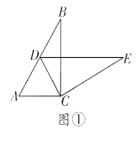
(1)如图①,智慧小组将![]() 绕点
绕点![]() 顺时针旋转,发现当点
顺时针旋转,发现当点![]() 恰好落在
恰好落在![]() 边上时,
边上时,![]() ,请你帮他们证明这个结论;
,请你帮他们证明这个结论;
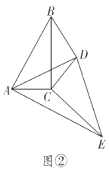
(2)缜密小组在智慧小组的基础上继续探究,连接![]() ,当
,当![]() C绕点
C绕点![]() 继续旋转到如图②所示的位置时,他们提出
继续旋转到如图②所示的位置时,他们提出![]() ,请你帮他们验证这一结论是否正确,并说明理由;
,请你帮他们验证这一结论是否正确,并说明理由;
探索发现
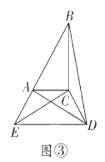
(3)如图③,勤奋小组在前两个小组的启发下,继续旋转![]() ,当
,当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
(4)在图①的基础上,写出一个边长比为![]() 的三角形(可添加字母).
的三角形(可添加字母).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图

根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
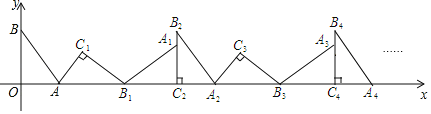
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(![]() ,0)、B(0,4),则点B2020的横坐标为_____.
,0)、B(0,4),则点B2020的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
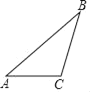
【题目】如图,已知△ABC,
(1)尺规作图:作AD平分∠BAC交BC于D点,再作AD的垂直平分线交AB于E点,交AC于F点(保留作图痕迹,不写作法);
(2)连接DE,DF证明:四边形AEDF是菱形;
(3)若BE=7,AF=4,CD=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:![]() . 设这种产品每天的销售利润为w元.
. 设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣![]() x2+
x2+![]() x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<
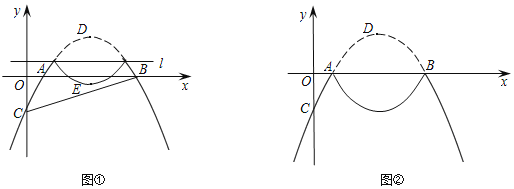
x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<![]() )上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
)上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
(1)求点A,B,D的坐标
(2)如图①,抛物线翻折后,点D落在点E处.当点E在△ABC内(含边界)时,求t的取值范围;
(3)如图②,当t=0时,若Q是“M”形新图象上一动点,是否存在以CQ为直径的圆与x轴相切于点P?若存在,直接写出出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |