
【题目】《郑州市城市生活垃圾分类管理办法》已于2019年12月1日起施行,为了解市民对垃圾分类的执行程度,某数学兴趣小组对部分市民进行了问卷调查,调查结果分为“A完全做到”“B基本做到”“C偶尔做到”“D很少做到”四类,该小组绘制的统计图如右:

(1)图中最大的扇形表示调查结果为 的市民占所有被调查市民的 %,这个扇形的圆心角为 °;
(2)你从图中还能得到哪些信息?(写出一条即可)
【答案】(1)B基本做到,45,162;(2)所有被调查市民中的大部分(![]() )市民可以达到B类以上.(注:此问答案不唯一)
)市民可以达到B类以上.(注:此问答案不唯一)
【解析】
(1)先比较各扇形所表示的百分比的大小,再根据圆心角的计算方法求解即可;
(2)计算A、B两类所占比例之和,得出相应结论即可.
(1)观察扇形统计图可知:![]()
所以图中最大的扇形表示的调查结果为“B基本做到”的市民,其占所有被调查市民的![]()
这个扇形的圆心角为:![]()
故答案为:B基本做到,45,162;
(2)从扇形统计图可知:“A完全做到”的市民占所有被调查市民的![]() ,“B基本做到”的市民占所有被调查市民的
,“B基本做到”的市民占所有被调查市民的![]()
两者之和为![]()
这表明所有被调查市民中的大部分(![]() )市民可以达到B类以上.(注:此问答案不唯一)
)市民可以达到B类以上.(注:此问答案不唯一)


科目:初中数学 来源: 题型:
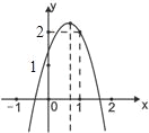
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2.若S=3,则S1+S2的值为( )

A. 3 B. 6 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与设计:
在图1和图2中,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.

(1)在图1中以格点为顶点画一个三角形,使三角形三边长分别为![]() ,
,![]() ,4;
,4;
(2)在图2中以格点为顶点画一个面积为10的正方形;
(3)在图3的正方形网格中建立平面直角坐标系,若![]() 各顶点的坐标分别为:
各顶点的坐标分别为:![]() ,
,![]() ,
,![]() ,请你作
,请你作![]() ,使
,使![]() 和
和![]() 关于
关于![]() 轴对称.
轴对称.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为![]() 元的某种商品原来按每件
元的某种商品原来按每件![]() 元出售,一天可售出
元出售,一天可售出![]() 件.后来经过市场调查,发现这种商品单价每降低
件.后来经过市场调查,发现这种商品单价每降低![]() 元,其销量可增加
元,其销量可增加![]() 件.
件.
![]() 求商场经营该商品原来一天可获利润多少元?
求商场经营该商品原来一天可获利润多少元?
![]() 若商场经营该商品一天要获利润
若商场经营该商品一天要获利润![]() 元,并让顾客得到实惠,则每件商品应降价多少元?
元,并让顾客得到实惠,则每件商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com