
【题目】在一条直线上依次有A,B,C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.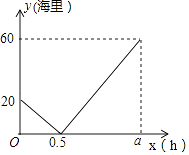
(1)A,C两港口间的距离为海里,a=
(2)求y与x之间的函数关系式.
(3)在B岛上有一个不间断发射信号的信号发射台,发射的信号覆盖半径为8海里的圆形区域,求该海巡船鞥接受到该信号的时间有多长?
【答案】
(1)80,2h
(2)解:当0<x≤0.5时,设y与x的函数关系式为:y=kx+b,
∵函数图象经过点(0,20),(0.5,0)
∴ ![]() ,
,
解得 ![]() .
.
所以,y=﹣0x+20;
当0.5<x≤1.7时,设y与x的函数关系式为:y=mx+n,
∵函数图象经过点(0.5,0),(2,60),
∴ ![]() ,
,
解得 ![]() .
.
所以,y=40x﹣20,
(3)解:当0≤x≤0.5,y=8时,﹣40x+20=8,
解得x=0.3,
当0.5<x≤2,y=8时,40x﹣20=8,
解得x=0.7,
∴0.7﹣0.3=0.4
答:该海巡船能接受到该信号的时间为:0.4h.
【解析】解:(1)由图可知,A、B港口间的距离为20,B、C港口间的距离为60,
所以,A、C港口间的距离为:20+60=80km,
海巡船的速度为:20÷0.5=40km/h,
∴a=80÷40=2h,
所以答案是:80,2h;


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图1,![]() 直线
直线![]() 分别交
分别交![]() 于点
于点![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() 与
与![]() 交于点
交于点![]() 交
交![]() 于
于![]() .
.

(1)求证:![]()
(2)如图2,连接![]() 为
为![]() 上一动点,
上一动点,![]() 平分
平分![]() 交
交![]() 于
于![]() 则
则![]() 的大小是否发生变化?若不变,求出其值;若改变,请说明理由.
的大小是否发生变化?若不变,求出其值;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠MON=90°,点A,B分别在OM、ON上运动(不与点O重合).
(1)如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB= °
(2)如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D
①若∠BAO=60°,则∠D= °.
②随着点A,B的运动,∠D的大小会变吗?如果不会,求∠D的度数;如果会,请说明理由.
(3)如图③,延长MO至Q,延长BA至G,已知∠BAO,∠OAG的平分线与∠BOQ的平分线及其延长线相交于点E、F,在△![]() 中,如果有一个角是另一个角的3倍,求∠ABO的度数.
中,如果有一个角是另一个角的3倍,求∠ABO的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.若AC=4,则EG2+FH2=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;

(2)补全条形统计图;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PC=2PB.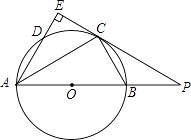
(1)探究线段PB,AB之间的数量关系,并说明理由;
(2)若AD=3,求AB长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知, 四边形![]() , 连接
, 连接![]() ,
,![]() ,
,![]() .
.
(1)如图![]() , 求证:
, 求证:![]() 平分
平分![]() ;
;
(2)如图![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在![]() 的条件下,连接
的条件下,连接![]() ,点
,点![]() 在
在![]() 延长线上,连接
延长线上,连接![]() ,延长
,延长![]() 与
与![]() 延长线交于点
延长线交于点![]() , 若
, 若![]() ,
,![]() ,
, ![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]() ,
, ![]() ,
,![]() ,求
,求![]() 的长.
的长.
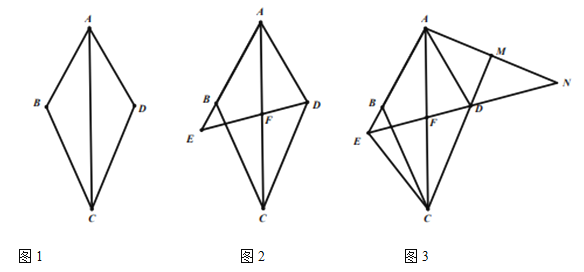
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com