
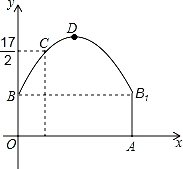
.如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣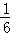 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为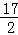 m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
【考点】二次函数的应用.
【专题】压轴题.
【分析】(1)先确定B点和C点坐标,然后利用待定系数法求出抛物线解析式,再利用配方法确定顶点D的坐标,从而得到点D到地面OA的距离;
(2)由于抛物线的对称轴为直线x=6,而隧道内设双向行车道,车宽为4m,则货运汽车最外侧与地面OA的交点为(2,0)或(10,0),然后计算自变量为2或10的函数值,再把函数值与6进行大小比较即可判断;
(3)抛物线开口向下,函数值越大,对称点之间的距离越小,于是计算函数值为8所对应的自变量的值即可得到两排灯的水平距离最小值.
【解答】解:(1)根据题意得B(0,4),C(3,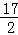 ),
),
把B(0,4),C(3,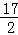 )代入y=﹣
)代入y=﹣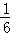 x2+bx+c得
x2+bx+c得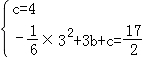 ,
,
解得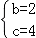 .
.
所以抛物线解析式为y=﹣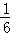 x2+2x+4,
x2+2x+4,
则y=﹣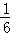 (x﹣6)2+10,
(x﹣6)2+10,
所以D(6,10),
所以拱顶D到地面OA的距离为10m;
(2)由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y= >6,
>6,
所以这辆货车能安全通过;
(3)令y=8,则﹣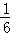 (x﹣6)2+10=8,解得x1=6+2
(x﹣6)2+10=8,解得x1=6+2 ,x2=6﹣2
,x2=6﹣2 ,
,
则x1﹣x2=4 ,
,
所以两排灯的水平距离最小是4 m.
m.
【点评】本题考查了二次函数的应用:构建二次函数模型解决实际问题,利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
池塘中放养了鲤鱼2000条,鲢鱼若干,在几次随机捕捞中,共抓到鲤鱼400条,鲢鱼800条,估计池塘中原来放养了鲢鱼( )条.
A.1000 B.2000 C.3000 D.4000
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,甲袋内共有4张牌,牌面分别标记数字1,2,3,4;乙袋内共有3张牌,牌面分别标记数字2,3,4。甲袋中每张牌被取出的机会相等,且乙袋中每张牌被取出的机会也相等。分别从甲乙两袋中各随机抽取一张牌,请用列表或画树形图的方法,求抽出的两张牌面上的数字之和大于5的概率。
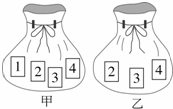 |
查看答案和解析>>
科目:初中数学 来源: 题型:
对于每个非零自然数n,抛物线y=x2﹣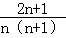 x+
x+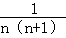 与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2015B2015的值是( )
与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2015B2015的值是( )
A.1 B.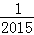 C.
C.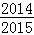 D.
D.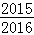
查看答案和解析>>
科目:初中数学 来源: 题型:
青蛙是我们人类的朋友,为了了解某池塘里青蛙的数量,先从池塘里捕捞20只青蛙,作上标记后放回池塘,经过一段时间后,再从池塘中捕捞出40只青蛙,其中有标记的青蛙有4只,请你估计一下这个池塘里有多少只青蛙?
A.100只 B.150只 C.180只 D.200只
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com