
【题目】甲、乙两车从 A,B 两地同时出发,沿同一条路线相向匀速行驶.出发后经 2 小时两车相遇, 已知在相遇时乙车比甲车多行驶了 30 千米.相遇后若乙车继续往前行驶,还需 1.6 小时才能 到达 A 地.
(1)求甲,乙两车行驶的速度分别是多少?
(2)如果相遇后甲车继续前往 B 地(到达后停止行驶),乙车在相遇点休息了 10 分钟后,按 原速度立即返回 B 地,问乙车重新出发后多长时间,两车相距 5 千米?
【答案】(1)甲的速度为60千米/小时,乙的速度为75千米/小时;(2)![]() 小时或1小时.
小时或1小时.
【解析】
(1)设甲的速度为每小时![]() 千米,则乙的速度为每小时(x+
千米,则乙的速度为每小时(x+![]() )千米,根据“相遇后若乙车继续往前行驶,还需 1.6 小时才能 到达 A 地”,可知甲2小时行驶的路程等于乙1.6 小时行驶的路程,列出方程求出甲的速度,进而可得乙的速度;
)千米,根据“相遇后若乙车继续往前行驶,还需 1.6 小时才能 到达 A 地”,可知甲2小时行驶的路程等于乙1.6 小时行驶的路程,列出方程求出甲的速度,进而可得乙的速度;
(2)设乙车重新出发后![]() 小时两车相距5千米,分两种情况:若乙车在甲车后5千米,则甲(y+
小时两车相距5千米,分两种情况:若乙车在甲车后5千米,则甲(y+![]() )小时行驶的路程=乙y 小时行驶的路程+5;若乙车在甲车前5千米,则乙y小时行驶的路程-5=甲(y+
)小时行驶的路程=乙y 小时行驶的路程+5;若乙车在甲车前5千米,则乙y小时行驶的路程-5=甲(y+![]() ) 小时行驶的路程,列出方程求解即可.
) 小时行驶的路程,列出方程求解即可.
(1)设甲的速度为每小时![]() 千米,则乙的速度为每小时(x+
千米,则乙的速度为每小时(x+![]() )千米
)千米
由题意可得2x=1.6(x+![]() )
)
解得x=60
∴x+![]() =75
=75
答:甲的速度为60千米/小时,乙的速度为75千米/小时.
(2)设乙车重新出发后y小时两车相距5千米
乙车重新出发后,甲车到达![]() 地还需要的时间为
地还需要的时间为![]() =
=![]() 小时
小时
若乙车在甲车后5千米,
则75y+5=60(y+![]() )
)
解得y=![]()
若乙车在甲车前5千米
则75y-5=60(y+![]() )
)
解得![]()
即乙车重新出发后经过![]() 小时或1小时两车相距5千米.
小时或1小时两车相距5千米.
故答案为:(1)甲的速度为60千米/小时,乙的速度为75千米/小时;(2)![]() 小时或1小时.
小时或1小时.


科目:初中数学 来源: 题型:
【题目】水是人类的生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数 1 至 1050 按一定规律排列如下表:
1 | 2 | 3 | 4 | 5 | 6 | 7 |
8 | 9 | 10 | 11 | 12 | 13 | 14 |
15 | 16 | 17 | 18 | 19 | 20 | 21 |
22 | 23 | 24 | 25 | 26 | 27 | 28 |
29 | 30 | 31 | 32 | 33 | 34 | 35 |
从表中任取一个 3 3 的方框(如表中带阴影的部分),方框中九个数的和可能是( )
A. 2025 B. 2018 C. 2016 D. 2007
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG=cm. 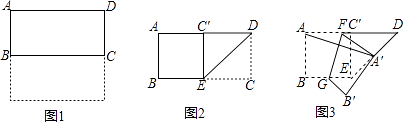
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司推出一款移动话费套餐,资费标准见下表:
套餐月费/元 | 套餐内容 | 套餐外资费 | |
主叫限定时间/分钟 | 被叫 | 主叫超时费 (元/分钟) | |
58 | 50 | 免费 | 0.25 |
88 | 150 | 0.20 | |
118 | 350 | 0.15 | |
说明:①主叫:主动打电话给别人;被叫:接听别人打进来的电话. ②若办理的是月使用费为 58 元的套餐,主叫时间不超过 50 分钟时,当月话费即 为 58 元;主叫时间为 60 分钟,则当月话费为 58+0.25×(60-50)=60.5 元. | |||
小文办理的是月使用费为 88 元的套餐,亮亮办理的是月使用费为 118 元的套餐.
(1)小文当月的主叫时间为 220 分钟,则该月她的话费需多少元?
(2)某月小文和亮亮的主叫时间都为 m 分钟 (m 350) ,请用含 m 的代数式表示该月他们的 话费差.
(3)某月小文和亮亮的话费相同,但主叫时间比亮亮少 100 分钟,求小文和亮亮的主叫时间 分别为多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:
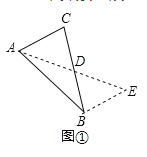

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数 y=2x 与 y=ax+5 的图象相交于点 A(m,4).
(1)求 A 点坐标及一次函数 y=ax+5 的解析式;
(2)设直线 y=ax+5 与 x 轴交于点 B,求△AOB 的面积;
(3)求不等式 2x<ax+5 的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com