
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.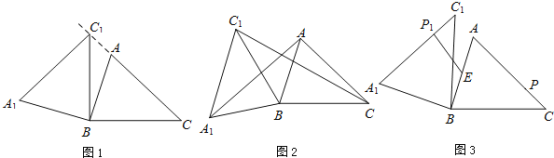
【答案】(1)∠CC1A1=90°.
(2)S△CBC1=![]() .
.
(3)最小值为:EP1=![]() ﹣2.
﹣2.
最大值为:EP1= 7.
【解析】
(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,又由等腰三角形的性质,即可求得∠CC1A1的度数.
(2)由旋转的性质可得:△ABC≌△A1BC1,易证得△ABA1∽△CBC1,利用相似三角形的面积比等于相似比的平方,即可求得△CBC1的面积.
(3)由①当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,即可求得线段EP1长度的最大值与最小值.
解:(1)∵由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°.
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.
(2)∵由旋转的性质可得:△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1.
∴![]() ,∠ABC+∠ABC1=∠A1BC1+∠ABC1
,∠ABC+∠ABC1=∠A1BC1+∠ABC1
∴∠ABA1=∠CBC1.
∴△ABA1∽△CBC1
∴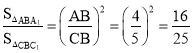 .
.
∵S△ABA1=4,∴S△CBC1=![]() .
.
(3)过点B作BD⊥AC,D为垂足,

∵△ABC为锐角三角形,∴点D在线段AC上.
在Rt△BCD中,BD=BC×sin45°=![]() .
.
①如图1,当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小.最小值为:EP1=BP1﹣BE=BD﹣BE=![]() ﹣2.
﹣2.
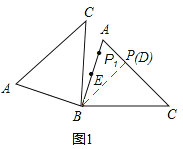
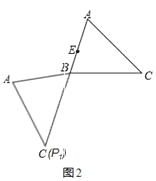
②如图2,当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大.最大值为:EP1=BC+BE=5+2=7.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
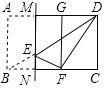
【题目】如图,在矩形ABCD中,AB:BC=3:5,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
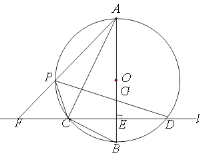
【题目】如图,在⊙O的内接三角形ABC中,![]() ,
,![]() ,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是
,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是![]() 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
(1)求证:![]() ;
;
(2)若![]() ,
, ![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
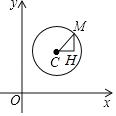
【题目】在平面直角坐标系中,以C(x0,y0)为圆心半径为r的圆的标准方程是(x﹣x0)2+(y﹣y0)2=r2.例如,在平面直角坐标系中,⊙C的圆心C(2,3),点M(3,5)是圆上一点,如图,过点C、点M分别作x轴、y轴的平行线,交于点H,在Rt△MCH中,由勾股定理可得:r2=MC2=CH2+MH2=1+4=5,则圆C的标准方程是(x﹣2)2+(y﹣3)2=5.那么以点(﹣3,4)为圆心,过点(﹣2,﹣1)的圆的标准方程是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x﹣a)(x+5)=x2﹣bx﹣5,一元二次方程ax2+bx+k=0的两个实数根x1,x2满足![]() (x1﹣x2)2﹣2x1x2=4,则k=_____.
(x1﹣x2)2﹣2x1x2=4,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
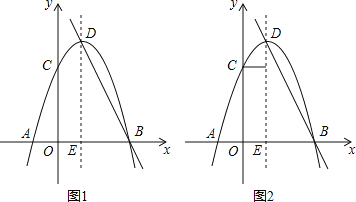
【题目】关于x的一元二次方程(m+1)x2+2(m+1)x+2=0有两个相等的实数根,抛物线y=﹣x2+(m+1)x+3与x轴交于A、B两点(A在B左侧),与y轴相交于点C,抛物线的顶点为D.
(1)求抛物线的解析式.
(2)如图1,设抛物线的对轴交x轴于点E,在抛物线的对称轴上是否存在点P,使P点到x轴的距离等于P点到直线BD的距离?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图2,作CF⊥DE于F,M为射线EA上一动点.如果在线段EF上恰好存在两个点N满足△CFN与△NEM相似,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
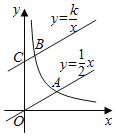
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移2个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=3BC,则k的值为____.
x向上平移2个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=3BC,则k的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,阿基米德流传于世的著作有10余种,多为希腊文手稿下面是《阿基米德全集》中记载的一个命题:AB是⊙O的弦,点C在⊙O上,且CD⊥AB于点D,在弦AB上取点E,使AD=DE,点F是![]() 上的一点,且
上的一点,且![]() =
=![]() ,连接BF可得BF=BE.
,连接BF可得BF=BE.
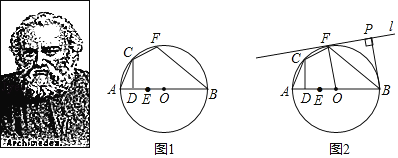
(1)将上述问题中弦AB改为直径AB,如图1所示,试证明BF=BE;
(2)如图2所示,若直径AB=10,EO=![]() OB,作直线l与⊙O相切于点F.过点B作BP⊥l于点P.求BP的长.
OB,作直线l与⊙O相切于点F.过点B作BP⊥l于点P.求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com