
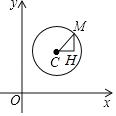
����Ŀ����ƽ��ֱ������ϵ�У���C��x0��y0��ΪԲ�İ뾶Ϊr��Բ�ı������ǣ�x��x0��2+��y��y0��2��r2�����磬��ƽ��ֱ������ϵ�У���C��Բ��C��2��3������M��3��5����Բ��һ�㣬��ͼ������C����M�ֱ���x�ᡢy���ƽ���ߣ����ڵ�H����Rt��MCH�У��ɹ��ɶ����ɵã�r2��MC2��CH2+MH2��1+4��5����ԲC�ı������ǣ�x��2��2+��y��3��2��5����ô�Ե㣨��3��4��ΪԲ�ģ����㣨��2����1����Բ�ı�������_____��
���𰸡�26
��������
����ͼ������������ȷ��Բ�ı����̵Ľ���ʽ�ǣ�x��x0��2+��y��y0��2��r2�����У�x0��y0����Բ�ģ�r��MC֮��ľ��룬���ù��ɶ������r�ij��ȼ��ɽ���.
�⣺��ͼ��Բ��C����3��4������M����2����1������C��CH��x�ᣬ��M��MH��y�ᣬCH��MH�ڵ�H��
����Rt��MCH��CH����2������3����1��MH��4������1����5��
��r2��MC2��CH2+MH2��1+25��26��
���Ե㣨��3��4��ΪԲ�ģ����㣨��2����1����Բ�ı������ǣ�x+3��2+��y��4��2��26��
�ʴ�Ϊ����x+3��2+��y��4��2��26��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
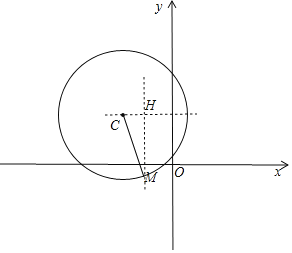
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�O������ԭ�㣮��A��x����������ϣ���A������Ϊ��10��0����һ��������![]() ����O��A��B���㣬ֱ��AB�ı���ʽΪ
����O��A��B���㣬ֱ��AB�ı���ʽΪ![]() �����������ߵĶԳ��ύ�ڵ�Q��
�����������ߵĶԳ��ύ�ڵ�Q��
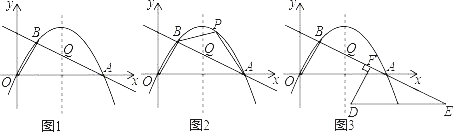
��1���������ߵı���ʽ��
��2����ͼ2����A��B����֮�������������һ����P������AP��BP�����P�ĺ�����Ϊm����ABP�����S��������Sȡ�����ֵʱ��P�����ꣻ
��3����ͼ3������OAB������BA����ƽ�Ƶõ���DEF����ƽ�ƹ����У���A��D��QΪ������������ܷ��Ϊ���������Σ�����ܣ���ֱ��д����ʱ��E�����꣨��O���⣩��������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
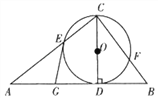
����Ŀ����ͼ����֪CD�ǡ�ABC��AB���ϵĸߣ���CDΪֱ���ġ�O�ֱ�CA, CB�ڵ�E��F����G��AD���е㣮��֤��GE�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���뾶Ϊ1��Բ�Ľ�Ϊ60��������ֽƬOAB��ֱ��L�������������Ĺ������ҹ���������O��A��B��������O��������·���ܳ��� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı߳�Ϊ20cm����ABC=120�����Խ���AC��BD�ཻ�ڵ�O������P�ӵ�A��������4cm/s���ٶȣ���A��B��·�����B�˶�������P��PQ��BD����AC�ཻ�ڵ�Q�����˶�ʱ��Ϊt�룬0��t��5��

��1�����ı���PQCB�����ΪS����S��t�Ĺ�ϵʽ��
��2������Q����O�ĶԳƵ�ΪM������P�Ҵ�ֱ��AB��ֱ��l������ABCD�ı�AD����CD���ڵ�N����tΪ��ֵʱ����P��M��N��һֱ���ϣ�
��3��ֱ��PN��AC�ཻ��H�㣬����PM��NM���Ƿ����ijһʱ��t��ʹ��ֱ��PNƽ���ı���APMN������������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ABC�У�AB=4��BC=5����ACB=45��������ABC�Ƶ�B����ʱ�뷽����ת���õ���A1BC1��
��1����ͼ1������C1���߶�CA���ӳ�����ʱ�����CC1A1�Ķ�����
��2����ͼ2������AA1��CC1������ABA1�����Ϊ4������CBC1�������
��3����ͼ3����EΪ�߶�AB�е㣬��P���߶�AC�ϵĶ��㣬����ABC�Ƶ�B����ʱ�뷽����ת�����У���P�Ķ�Ӧ���ǵ�P1�����߶�EP1���ȵ����ֵ����Сֵ��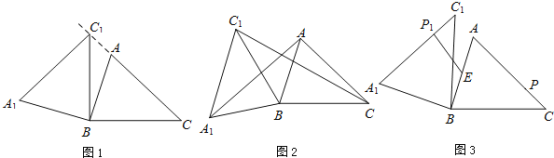
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿѧ�����������ʣ������������Ź涨ѧ��ÿ��μӻ�����ƽ��ʱ�䲻����1Сʱ��Ϊ�˽�ѧ���μӻ�����������Բ���ѧ���μӻ�����ʱ����г������飬����������������������������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
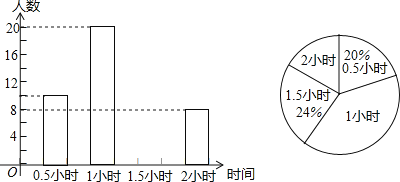
��1������ε����й������˶�����ѧ����
��2������Ƶ���ֲ�ֱ��ͼ��
��3�����ʾ����ʱ�� 1Сʱ������Բ�ĽǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
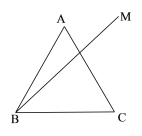
����Ŀ����ͼ���ȱߡ�ABC�У�BM��ABC�ڲ���һ�����ߣ���![]() ����A����BM�ĶԳƵ�ΪD������AD��BD��CD������AD��CD���ӳ��߷ֱ�����BM�ڵ�E��P��
����A����BM�ĶԳƵ�ΪD������AD��BD��CD������AD��CD���ӳ��߷ֱ�����BM�ڵ�E��P��
(1)�����ⲹȫͼ�Σ�
(2)��ABM ����BDC �Ĵ�С���ú���ʽ�ӱ�ʾ����
(3)�õ�ʽ��ʾ�߶�PB��PC��PE֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
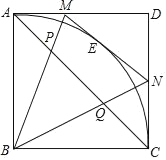
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1����E�ǻ�AC�ϵ�һ�����㣬����E��������AD���ڵ�M����CD���ڵ�N��
��1����֤����MBN��45����
��2����AM��x��CN��y����y����x�ĺ�����ϵʽ��
��3���������εĶԽ���AC��BM��P��BN��Q�����AP��m��CQ��n����m��n֮������Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com