
【题目】如图,正方形ABCD的边长为1,点E是弧AC上的一个动点,过点E的切线与AD交于点M.与CD交于点N.
(1)求证:∠MBN=45°;
(2)设AM=x,CN=y,求y关于x的函数关系式;
(3)设正方形的对角线AC交BM于P,BN于Q,如果AP=m,CQ=n,求m与n之间满足的关系式.
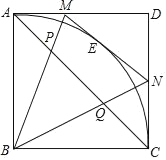
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接BE,证明Rt△ABM≌Rt△EBM(HL),即可得∠ABM=∠EBM,再证明Rt△CBN≌Rt△EBN,即可证明∠CBN=∠EBN,再根据∠ABM+∠EBM+∠EBN+∠CBN=90°,即可证明∠MBN=45°.
(2)根据(1)得MN=x+y,MD=1﹣x,ND=1﹣y.再根据勾股定理列方程化简即可得到y关于x的函数关系式.
(3)根据△ABQ∽△BPQ和△CBP∽△BQP列出相似比,再根据相似比可得![]() ,代入计算即可.
,代入计算即可.
证明:(1)如图,连接BE,
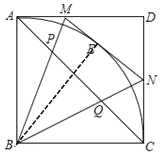
∵MN是⊙B的切线
∴BE⊥MN,
∵AB=BE,BM=BM
∴Rt△ABM≌Rt△EBM(HL)
∴∠ABM=∠EBM,
同理可证:Rt△CBN≌Rt△EBN
∴∠CBN=∠EBN
∵∠ABC=90°
∴∠ABM+∠EBM+∠EBN+∠CBN=90°
∴2(∠MBE+∠NBE)=90°
∴∠MBN=45°
(2)∵Rt△ABM≌Rt△EBM,Rt△CBN≌Rt△EBN
∴AM=ME=x,CN=NE=y
∴MN=x+y,MD=1﹣x,ND=1﹣y
∵MD2+ND2=MN2,
∴(1﹣x)2+(1﹣y)2=(x+y)2,
∴1﹣2x+1﹣2y=2xy
∴y=![]()
(3)∵四边形ABCD是正方形
∴AB=BC=1,∠BAC=∠ACB=45°
∴AC=![]()
∵∠MBN=∠BAC=45°,∠AQB=∠AQB
∴△ABQ∽△BPQ
∴![]()
∴![]() ①
①
∵∠MBN=∠ACB=45°,∠CPB=∠BPQ
∴△CBP∽△BQP
∴![]()
∴![]() ②
②
由①②得:![]()
∴AC﹣CQ=![]()
∴![]() ﹣n=
﹣n=![]()
∴m=![]()


科目:初中数学 来源: 题型:
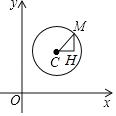
【题目】在平面直角坐标系中,以C(x0,y0)为圆心半径为r的圆的标准方程是(x﹣x0)2+(y﹣y0)2=r2.例如,在平面直角坐标系中,⊙C的圆心C(2,3),点M(3,5)是圆上一点,如图,过点C、点M分别作x轴、y轴的平行线,交于点H,在Rt△MCH中,由勾股定理可得:r2=MC2=CH2+MH2=1+4=5,则圆C的标准方程是(x﹣2)2+(y﹣3)2=5.那么以点(﹣3,4)为圆心,过点(﹣2,﹣1)的圆的标准方程是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
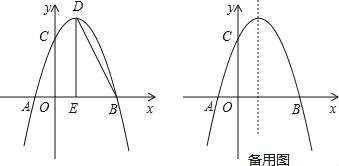
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接DB.
(1)求此抛物线的解析式及顶点D的坐标;
(2)点M是抛物线上的动点,设点M的横坐标为m.
①当∠MBA=∠BDE时,求点M的坐标;
②过点M作MN∥x轴,与抛物线交于点N,P为x轴上一点,连接PM,PN,将△PMN沿着MN翻折,得△QMN,若四边形MPNQ恰好为正方形,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
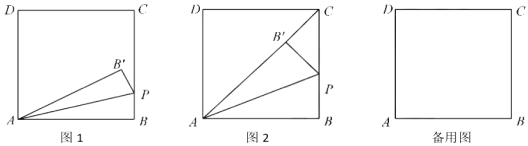
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代算书《九章算术》中第九章第六题是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深葭长各几何?你读懂题意了吗?请回答水深______尺,葭长_____尺.解:根据题意,设水深OB=x尺,则葭长OA'=(x+1)尺.可列方程正确的是( )
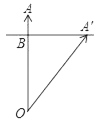
A. x2+52 =(x+1)2B. x2+52 =(x﹣1)2
C. x2+(x+1)2 =102D. x2+(x﹣1)2=52
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,阿基米德流传于世的著作有10余种,多为希腊文手稿下面是《阿基米德全集》中记载的一个命题:AB是⊙O的弦,点C在⊙O上,且CD⊥AB于点D,在弦AB上取点E,使AD=DE,点F是![]() 上的一点,且
上的一点,且![]() =
=![]() ,连接BF可得BF=BE.
,连接BF可得BF=BE.
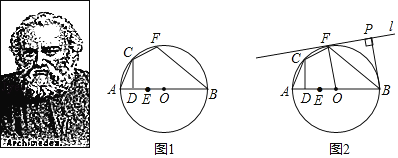
(1)将上述问题中弦AB改为直径AB,如图1所示,试证明BF=BE;
(2)如图2所示,若直径AB=10,EO=![]() OB,作直线l与⊙O相切于点F.过点B作BP⊥l于点P.求BP的长.
OB,作直线l与⊙O相切于点F.过点B作BP⊥l于点P.求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |
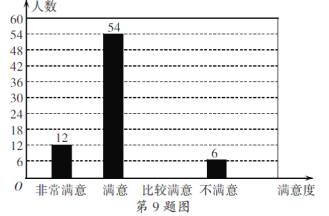
根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某八年级计划用360元购买笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,结果买得的笔记本比打折前多10本.
(1)请利用分式方程求出每本笔记本的原来标价;
(2)恰逢文具店周年志庆,每本笔记本可以按原价打8折,这样该校最多可购入本笔记本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com