
����Ŀ��Ϊ�˸��ο��ṩ���õķ���ij��������Բ����οͽ����˹��ڡ���������������ȡ��ĵ��飬�����ݵ��������Ƴ����²�������ͳ��ͼ��.
����� | ���� | ��ռ�ٷֱ� |
�dz����� | 12 | 10% |
���� | 54 | m |
�Ƚ����� | n | 40% |
������ | 6 | 5% |
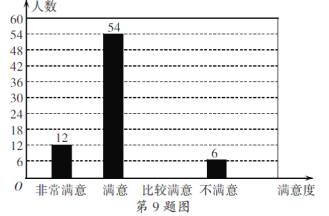
����ͼ����Ϣ������������⣺
(1)���ε����������Ϊ______������m��ֵΪ_______��
(2)�벹ȫ����ͳ��ͼ��
(3)��ͳ�ƣ��þ���ƽ��ÿ��Ӵ��ο�Լ3600�ˣ��������dz����⡱�͡����⡱��Ϊ�οͶԾ����������Ŀ϶���������Ƹþ���������ƽ��ÿ��õ��������ο͵Ŀ϶�.
���𰸡�(1)120��45%��(2)��ͼ��������(3)ƽ��ÿ��õ�Լ1980�˵Ŀ϶�.
��������
��1���dz��������������ռ�ٷֱȼ��㼴�ɵã�����������������������ɵ�m
��2��������Ƚ������n��ֵ��Ȼ��ȫ����ͼ����
��3��ÿ��Ӵ����ο������dz�����+���⣩�İٷֱȼ���
��1��12��10%=120��54��120��100%=45%
��2���Ƚ����⣺120��40%=48(��)����ȫ����ͳ��ͼ��ͼ.

(3)3600����45%+10%��=1980(��).
�𣺸þ���������ƽ��ÿ��õ�Լ1980�˵Ŀ϶�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿѧ�����������ʣ������������Ź涨ѧ��ÿ��μӻ�����ƽ��ʱ�䲻����1Сʱ��Ϊ�˽�ѧ���μӻ�����������Բ���ѧ���μӻ�����ʱ����г������飬����������������������������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
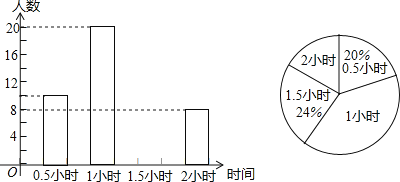
��1������ε����й������˶�����ѧ����
��2������Ƶ���ֲ�ֱ��ͼ��
��3�����ʾ����ʱ�� 1Сʱ������Բ�ĽǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ�����ʽ��������涨�����ʲ��Գɼ��ﵽ90.0�ּ����ϵ�Ϊ���㣻�ﵽ80.0����89.9�ֵ�Ϊ���ã��ﵽ60.0����79.9�ֵ�Ϊ����59.9�ּ�����Ϊ������ijУΪ���˽���꼶ѧ�����ʽ���״�����Ӹ�У���꼶ѧ���������ȡ��10%��ѧ���������ʲ��ԣ����Խ���������ͳ�Ʊ�������ͳ��ͼ��ʾ��
���ȼ�ѧ��ƽ����ͳ�Ʊ�
�ȼ� | ���� | ���� | ���� | ������ |
ƽ���� | 92.1 | 85.0 | 69.2 | 41.3 |
���ȼ�ѧ�������ֲ�����ͳ��ͼ

��1������ͳ��ͼ��������������ռ�İٷֱ��� ��;
��2����������ȡ��ѧ���IJ��Գɼ���ƽ���֣�
��3��������ȡ��ѧ�������в�����ȼ�ѧ�����ܷ�ǡ�õ���ijһ�����õȼ�ѧ���ķ���������Ƹþ��꼶ѧ����Լ�ж����˴ﵽ����ȼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1����E�ǻ�AC�ϵ�һ�����㣬����E��������AD���ڵ�M����CD���ڵ�N��
��1����֤����MBN��45����
��2����AM��x��CN��y����y����x�ĺ�����ϵʽ��
��3���������εĶԽ���AC��BM��P��BN��Q�����AP��m��CQ��n����m��n֮������Ĺ�ϵʽ��
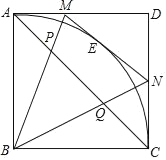
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽����
��ͼ1��������y��x2+![]() x+3��x�ύ��C��F���㣨��C�ڵ�F��ߣ�����y�ύ�ڵ�D��AD��2����B����Ϊ����4��5������EΪAB��һ�㣬��BE��ED������CD��CB��CE��
x+3��x�ύ��C��F���㣨��C�ڵ�F��ߣ�����y�ύ�ڵ�D��AD��2����B����Ϊ����4��5������EΪAB��һ�㣬��BE��ED������CD��CB��CE��
��1�����C��D��E�����ꣻ
��2����ͼ2���ӳ�ED��x���ڵ�M�����жϡ�CEM����״����˵�����ɣ�
��3����ͼ2�Ļ����ϣ�����CEM����CE���ۣ�ʹ��M���ڵ�M'�������жϵ�M'�Ƿ��ڴ��������ϣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������֣�
���ν���ǽ����ѧ�����һ����Ҫ��˼�뷽�����������ַ����ɽ��������ѧ֪ʶ���ֱ���������Ҿ��пɲ����ԣ��Ӷ����������ǿ��ٽ��⣮������ѧ���һЩ������ʽ���ܶ����ͨ����ʾ����ͼ������ķ�������ֱ���Ƶ��ͽ��ͣ����磺����ͼ�εļ���������֤��ȫƽ����ʽ����һ���߳�Ϊa�������εı߳�����b���γ��������κ����������Σ���ͼ1�����ͼ�ε�������Ա�ʾ�ɣ���a+b��2��a2+2ab+b2�ࣨa+b��2��a2+2ab+b2
�����֤�������͵���ȫƽ����ʽ��
���������
�������ͼ�μ�������ķ�����֤��13+23��32 ��ͼ2��A��ʾ1��1��1�������Σ�����1��1��1��13��B��ʾ1��2��2�������Σ�C��Dǡ�ÿ���ƴ��1��2��2�������Σ���ˣ�B��C��D�Ϳ��Ա�ʾ2��2��2�������Σ�����2��2��2��23����A��B��C��Dǡ�ÿ���ƴ��һ����1+2������1+2���Ĵ������Σ��ɴ˿ɵã�13+23����1+2��2��32
���Խ����
������������Ƶ����̣�����ͼ�μ������巽����֤��13+23+33���� ����Ҫ���Լ�����ͼ�β�д����֤���̣�
��ȹ��ɣ�
��������ı�ʾ����ͼ������ķ���̽����13+23+33+��+n3���� ����Ҫ��ֱ��д�����ۣ�����д��������̣�
ʵ��Ӧ�ã�
ͼ3�����ⳤΪ1��С�������ɵĴ������壬ͼ�д�С������һ���ж��ٸ���Ϊ����ȷ������С��������ܸ��������ǿ��Է���ͳ�ƣ����ֱ������ⳤ��1��2��3��4��������ĸ����������ܺͣ�
���磺�ⳤ��1���������У�4��4��4��43�����ⳤ��2���������У�3��3��3��33�����ⳤ��3���������У�2��2��2��23�����ⳤ��4���������У�1��1��l��13����Ȼ�����ã�3����ȹ��ɵĽ��ۣ��ɵã��������� ��ͼ4�����ⳤΪ1��С������ɵĴ������壬ͼ�д�С������һ������ ������
����Ӧ�ã�
������ⳤΪ1��С�������ɵĴ��������У�ͨ������ķ�ʽ�����Ĵ�С������һ����44100������ô�ⳤΪ1��С������һ������ ������
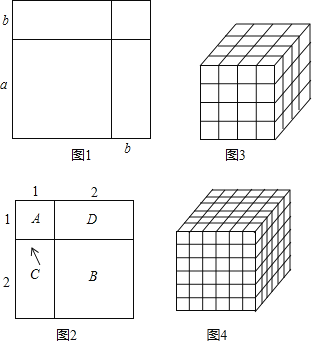
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
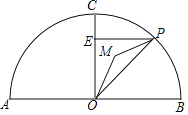
����Ŀ����ͼ��ABΪ��O��ֱ������AO��4����C�ڰ�Բ�ϣ�OC��AB������Ϊ��O��PΪ��Բ������һ���P����PE��OC�ڵ�E������OPE������ΪM������OM
��1�����OMP�Ķ�����
��2�����ŵ�P�ڰ�Բ��λ�õĸı䣬��CMO�Ĵ�С�Ƿ�ı䣬˵�����ɣ�
��3������P�ڰ�Բ�ϴӵ�B�˶�����Aʱ��ֱ��д������M��������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
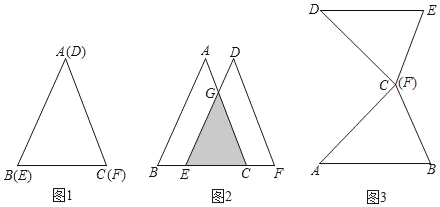
����Ŀ����ͼ1����֪������ֽƬ��ABC�͡�DEF�غ���һ��AB��AC��DE��DF����ABC�ա�DEF����ѧʵ����ϣ�����ʦ��ͬѧ����������ֽƬ�������²�����
(1)������̽��1�����֡�ABC����������DEF������BC����ƽ����ͼ2��ʾλ�ã�ͨ����������BE��CE��1��2����S��CGE��S��CAB���� ����
(2)������̽��2�����֡�ABC����������DEFͨ��һ��ȫ�ȱ任(ƽ�ơ���ת���ۺ�͡�ABCƴ����BCΪһ���Խ��ߵ����Σ����������������ȫ�ȱ任���̣�
(3)������̽��3�������������ΰ�ͼ3��ʾ���ã���C���F�غϣ�AB��DE�����֡�ABC����������DEF������DA����ƽ�ƣ���AB��13��BC��10�����DEFƽ�Ƶľ���Ϊm��
����m��0ʱ������AD��BE���ж��ı���ABED����״��˵�����ɣ�
����ƽ�ƵĹ����У��ı���ABED�ܷ��Ϊ�����Σ����ܣ������m��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ijУΪ�˽���꼶��ͬѧ����������������������ȡ������ͬѧ������1000���ܲ���.���ճɼ���Ϊ���㡢���á��ϸ��벻�ϸ��ĸ��ȼ�.ѧУ���������²�������ͳ��ͼ.
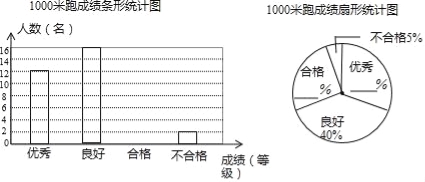
��1�����ݸ�������Ϣ����ȫ����ͳ��ͼ��
��2����У���꼶��600������������Ƴɼ�δ�ﵽ�����ж�����?
��3��ij��ס�����λ�ɼ������ͬѧ��ѡ�вμӼ������е�ѧУ�˶���1000�ױ�����Ԥ����ΪA��B��C������У�ѡ���ɳ�ǩȷ������.�ס�������ǡ�÷���ͬһ��ĸ����Ƕ���?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com