
����Ŀ���ۺ���̽����
��ͼ1��������y��x2+![]() x+3��x�ύ��C��F���㣨��C�ڵ�F��ߣ�����y�ύ�ڵ�D��AD��2����B����Ϊ����4��5������EΪAB��һ�㣬��BE��ED������CD��CB��CE��
x+3��x�ύ��C��F���㣨��C�ڵ�F��ߣ�����y�ύ�ڵ�D��AD��2����B����Ϊ����4��5������EΪAB��һ�㣬��BE��ED������CD��CB��CE��
��1�����C��D��E�����ꣻ
��2����ͼ2���ӳ�ED��x���ڵ�M�����жϡ�CEM����״����˵�����ɣ�
��3����ͼ2�Ļ����ϣ�����CEM����CE���ۣ�ʹ��M���ڵ�M'�������жϵ�M'�Ƿ��ڴ��������ϣ���˵�����ɣ�

���𰸡���1����C�������ǣ���4��0������D�������ǣ�0��3������E�������ǣ���![]() ��5������2����CEM�ĵ��������Σ����ɼ���������3����M'���ڴ��������ϣ����ɼ�����.
��5������2����CEM�ĵ��������Σ����ɼ���������3����M'���ڴ��������ϣ����ɼ�����.
��������
��1����������߽���ʽ��õ�C��D�����ꣻ��EA=a��������֪����BE=ED�г�����a2+22=��4-a��2���ⷽ�̼������a��ֵ���õ�E�����ꣻ
��2����CEM�ĵ��������Σ�����ȫ�������Σ���CBE�ա�CDE�������ʵõ���BEC=��CED����ƽ���ߵ����ʺ͵���������֪��CED=��ECM������EM=CM��֤����CEM�ĵ��������Σ�
��3����M'���ڴ��������ϣ���M��m��0���������������Σ���DOM�ס�DAE���Ķ�Ӧ�߳ɱ������m��ֵ����CM�ij��ȣ����ݷ��۵�����֪EM=EM�������ı���CMEM�������Σ������εĶԱ���ȵ����ʿ�����õ�M�������꣬��![]() ���뺯������ʽ������֤���ɣ�
���뺯������ʽ������֤���ɣ�
��1����ͼ1��ʾ��

��������y��x2+ ![]() x+3��x�ύ��C����y��0ʱ��x2+
x+3��x�ύ��C����y��0ʱ��x2+ ![]() x+3��0��
x+3��0��
���x1����![]() ��x2����4��
��x2����4��
�ߵ�C�ڵ�F��ߣ�
���C�������ǣ���4��0����
��x��0ʱ��y��3��
���D�������ǣ�0��3����
��AD��2��D��0��3����
��OA��5��
�ߵ�B����Ϊ����4��5����
��BA��x�ᣮ
��Rt��EAD����EA��a��EB��4��a��
��BE��ED��
��DE��4��a��
��a2+22����4��a��2����a��![]() ��
��
���E�������ǣ�![]() ��5����
��5����
��2����ͼ2��ʾ����CEM�ĵ��������Σ��������£�
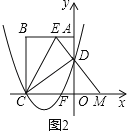
��C����4��0����D��0��3��֪��OC��4��OD��3��
�ɹ��ɶ������CD��5��
�֡ߵ�B����Ϊ����4��5����
��CB��5��CD��CB��
�֡�BE��BD��
���CBE�ա�CDE��SSS����
���BEC����CED��
�֡�BE��CM��
���BEC����ECM��
���CED����ECM��
��EM��CM��
���MCE�ǵ��������Σ�
��3����M'���ڴ��������ϣ��������£�
��ͼ3��ʾ��
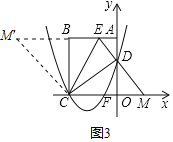
���M�������ǣ�m��0����
�ߡ�DOM�ס�DAE��
![]() ����
����![]()
���m��![]() ��
��
��CM��4+ ![]() ��
��![]() ��
��
�ɷ��ۿ�֪��EM��EM����
��CM��EM��
���ı���CMEM�������Σ�
��EM����CM��![]() ��
��
![]() ��
��
���M���������ǣ�![]() ��5����
��5����
��m��![]() ʱ�����������߽���ʽy��x2+
ʱ�����������߽���ʽy��x2+ ![]() x+3����
x+3����
 ��
��
���M�����ڴ��������ϣ�


 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯ѧ���鷨�������Բ�����Ʒ��A��B��C��D�ĸ��ȼ������������������ȡ����ѧ���鷨��Ʒ������������з���������������ͳ��ͼ������ͳ��ͼ���£�

����������Ϣ����������⣺
��1������γ�ȡ��������������
��2������ͼ���а�����ͳ��ͼ����������
��3����֪��У��λ���յ�������Ʒ750�ݣ�������Ʋ�����Ʒ�ﵽB�����ϣ���A����B�����ж��ٷݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y��x2+bx+c������1��3������4��0��
��1����������ߵĽ���ʽ����2������ֵy��0ʱ�Ա���x�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ����顶�����������еھ��µ������ǣ����гط�һ�ɣ����������룬��ˮһ�ߣ����縰�������밶�룬��ˮ���糤�����Σ����������������ش�ˮ��______�ߣ��糤_____�ߣ��⣺�������⣬��ˮ��OB��x�ߣ����糤OA'����x+1���ߣ����з�����ȷ���ǣ�������
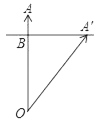
A. x2+52 ����x+1��2B. x2+52 ����x��1��2
C. x2+��x+1��2 ��102D. x2+��x��1��2��52
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() BF����ͬ����Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�E������EF�����ı���ABEF���ܳ�Ϊ16����C��60�㣬���ı���ABEF�������___��
BF����ͬ����Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�E������EF�����ı���ABEF���ܳ�Ϊ16����C��60�㣬���ı���ABEF�������___��
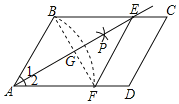
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��ο��ṩ���õķ���ij��������Բ����οͽ����˹��ڡ���������������ȡ��ĵ��飬�����ݵ��������Ƴ����²�������ͳ��ͼ��.
����� | ���� | ��ռ�ٷֱ� |
�dz����� | 12 | 10% |
���� | 54 | m |
�Ƚ����� | n | 40% |
������ | 6 | 5% |
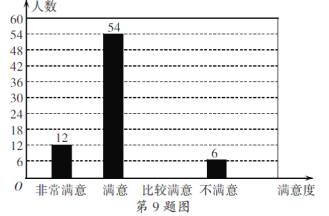
����ͼ����Ϣ������������⣺
(1)���ε����������Ϊ______������m��ֵΪ_______��
(2)�벹ȫ����ͳ��ͼ��
(3)��ͳ�ƣ��þ���ƽ��ÿ��Ӵ��ο�Լ3600�ˣ��������dz����⡱�͡����⡱��Ϊ�οͶԾ����������Ŀ϶���������Ƹþ���������ƽ��ÿ��õ��������ο͵Ŀ϶�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A. Ϊ�˽�ȫʡ��ѧ������������״�����˲����ղ鷽ʽ
B. ����ö�ʵؾ��ȵ�Ӳ�ң���öӲ�Ҷ������泯����һ�¼������ĸ���Ϊ![]()
C. ��һö�ʵؾ��ȵ����������ӣ�����ֹͣת����5�㳯���DZ�Ȼ�¼�
D. ������������ͬ�����¸����10�Σ����dzɼ���ƽ������ͬ������ֱ���S��2��0.4��S��2��0.6���������ɼ����ȶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��OΪ����ԭ�㣬�ı���OABCΪ���Σ�A��10��0����C��0��4������D��OA���е㣬��P��BC���˶�������ODP������Ϊ5�ĵ���������ʱ����P�������Ϊ�� ��

A. ��3��4����2��4�� B. ��2��4����8��4��
C. ��3��4����8��4�� D. ��3��4����2��4����8��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��������ȫ���������У����ж�ij·�ڵ����˽�ͨΥ�����������20��ĵ��飬�����õ����ݻ��Ƴ�����ͳ��ͼ��ͼ2����������
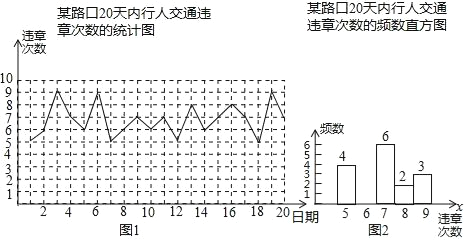
�����������Ϣ������������⣺
��1����13�죬��һ·�ڵ����˽�ͨΥ�´������� ������20���У����˽�ͨΥ��7�ε����� ���죮
��2����20���У����˽�ͨΥ��6�ε����� ���죻���ͼ2�е�Ƶ��ֱ��ͼ����������
��3���������ͼ2����һ������ͳ��ͼ����������Υ��9�ε�����������ͳ��ͼ�����Ե�Բ�ĽǶ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com